
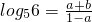 ;
;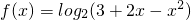 的值域是(0,2),其中正确说法的序号是________(注:把你认为是正确的序号都填上).
的值域是(0,2),其中正确说法的序号是________(注:把你认为是正确的序号都填上). 对称,
对称, =0,解之得a=-1,b=2,故①正确;
=0,解之得a=-1,b=2,故①正确; ,
,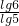 =
=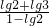 =
=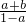 ,故④正确;
,故④正确;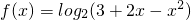 ≤log24=2,故函数函数
≤log24=2,故函数函数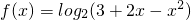 的值域是(-∞,2),故⑤不正确.
的值域是(-∞,2),故⑤不正确.

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
| π |
| 2 |
| 2π |
| 7 |
| π |
| 2 |
| π |
| 2 |
| π |
| 3 |
2tan
| ||
1-tan2
|
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x-1 |
| x+1 |
| 11 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| a |
| b |
查看答案和解析>>
科目:高中数学 来源: 题型:
下列说法中【 】
①若式子![]() 有意义,则x>1.
有意义,则x>1.
②已知∠α=27°,则∠α的补角是153°.
③已知x=2 是方程x2-6x+c=0 的一个实数根,则c 的值为8.
④在反比例函数![]() 中,若x>0
中,若x>0 ![]() 时,y 随x 的增大而增大,则k 的取值范围是k>2. 其中正确命题有
时,y 随x 的增大而增大,则k 的取值范围是k>2. 其中正确命题有
A. 1 个B. 2 个C. 3 个D. 4 个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com