
【题目】已知抛物线![]() 的准线与
的准线与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 作圆
作圆![]() 的两条切线,切点为
的两条切线,切点为![]() ,且
,且![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)若直线![]() 是过定点
是过定点![]() 的一条直线,且与抛物线
的一条直线,且与抛物线![]() 交于
交于![]() 两点,过定点
两点,过定点![]() 作
作![]() 的垂线与抛物线交于
的垂线与抛物线交于![]() 两点,求四边形
两点,求四边形![]() 面积的最小值.
面积的最小值.
科目:高中数学 来源: 题型:
【题目】如图,有一矩形钢板ABCD缺损了一角(如图所示),边缘线OM上每一点到点D的距离都等于它到边AB的距离.工人师傅要将缺损的一角切割下来使剩余部分成一个五边形,若AB=1m,AD=0.5m,则五边形ABCEF的面积最大值为____m2.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() ,
, ![]() ).
).
(1)当![]() 时,若
时,若![]() 在其定义域内为单调函数,求
在其定义域内为单调函数,求![]() 的取值范围;
的取值范围;
(2)当![]() 时,是否存在实数
时,是否存在实数![]() ,使得当
,使得当![]() 时,不等式
时,不等式![]() 恒成立,如果存在,求
恒成立,如果存在,求![]() 的取值范围,如果不存在,说明理由.
的取值范围,如果不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,甲船由A岛出发向北偏东45°的方向作匀速直线航行,速度为![]() nmile/h,在甲船从A岛出发的同时,乙船从A岛正南
nmile/h,在甲船从A岛出发的同时,乙船从A岛正南![]() nmile处的B岛出发,朝北偏东30°的方向作匀速直线航行,速度为
nmile处的B岛出发,朝北偏东30°的方向作匀速直线航行,速度为![]() nmile/h.
nmile/h.

(1)若两船能相遇,求m;
(2)当![]() 时,两船出发2小时后,求两船之间的距离.
时,两船出发2小时后,求两船之间的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
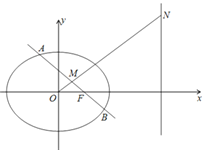
【题目】已知椭圆C1:![]() +
+![]() =1(a>b>0)的右焦点F(1,0),右准线l:x=4.圆C2:x2+y2=b2.A、B为椭圆上不同的两点,AB中点为M.
=1(a>b>0)的右焦点F(1,0),右准线l:x=4.圆C2:x2+y2=b2.A、B为椭圆上不同的两点,AB中点为M.
(1)求椭圆C1的方程;
(2)若直线AB过F点,直线OM交l于N点,求证:NF⊥AB;
(3)若直线AB与圆C2相切,求原点O到AB中垂线的最大距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com