[题目]已知等差数列{an}的前n项和为Sn . 且S3=9.a2a4=21.数列{bn}满足 .若 .则n的最小值为( )A.6B.7C.8D.9 题目和参考答案——青夏教育精英家教网—

【题目】已知等差数列{an}的前n项和为Sn ，且S3=9，a2a4=21，数列{bn}满足，若，则n的最小值为（）
A.6
B.7
C.8
D.9

【答案】C
【解析】解：设等差数列{an}的公差为d，∵S3=9，a2a4=21，∴3a1+ d=9，（a1+d）（a1+3d）=21，
联立解得：a1=1，d=2．
∴an=1+2（n﹣1）=2n﹣1．
∵数列{bn}满足，
∴n=1时， =1﹣ ，解得b1= ．
n≥2时， +…+ =1﹣ ，
∴ = ．
∴bn= ．
若，则＜．
n=7时，＞．
n=8时，＜．
因此：，则n的最小值为8．
故选：C．
【考点精析】认真审题，首先需要了解等差数列的通项公式（及其变式）(通项公式：或)．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】某高校调查了200名学生每周的自习时间（单位：小时），制成了如图所示的频率分布直方图，其中自习时间的范围是[17.5，30]，样本数据分组为[17.5，20），[20，22.5），[22.5，25），[25，27.5），[27.5，30]．根据直方图，若这200名学生中每周的自习时间不超过m小时的人数为164，则m的值约为（）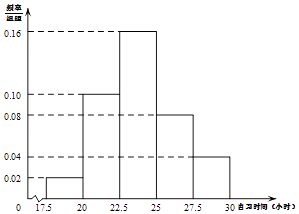
A.26.25
B.26.5
C.26.75
D.27

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知f（x）=ln（ax+b）+x2（a≠0）．
（1）若曲线y=f（x）在点（1，f（1））处的切线方程为y=x，求a，b的值；
（2）若f（x）≤x2+x恒成立，求ab的最大值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】宿州市某登山爱好者为了解山高y（百米）与气温x（℃）之间的关系，随机统计了4次山高与相应的气温，并制作了对照表，由表中数据，得到线性回归方程为y=﹣2x+a，由此估计山高为72（百米）处的气温为（）

气温x（℃）	18	13	10	﹣1
山高y（百米）	24	34	38	64

A.﹣10
B.﹣8
C.﹣6
D.﹣4

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】共享单车进驻城市，绿色出行引领时尚，某市有统计数据显示，2016年该市共享单车用户年龄等级分布如图1所示，一周内市民使用单车的频率分布扇形图如图2所示，若将共享单车用户按照年龄分为“年轻人”（20岁～39岁）和“非年轻人”（19岁及以下或者40岁及以上）两类，将一周内使用的次数为6次或6次以上的称为“经常使用单车用户”，使用次数为5次或不足5次的称为“不常使用单车用户”，已知在“经常使用单车用户”中有是“年轻人”．
（Ⅰ）现对该市市民进行“经常使用共享单车与年龄关系”的调查，采用随机抽样的方法，抽取一个容量为200的样本，请你根据图表中的数据，补全下列2×2列联表，并根据列联表的独立性检验，判断能有多大把握可以认为经常使用共享单车与年龄有关？
使用共享单车情况与年龄列联表