
 解:如图,建立平面直角坐标系,由题意可设A、B两人速度分别为3v千米/小时,
解:如图,建立平面直角坐标系,由题意可设A、B两人速度分别为3v千米/小时, ,得
,得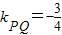 .
. 与圆O:x2+y2=9相切,
与圆O:x2+y2=9相切, =3,b=
=3,b=
 千米处.
千米处.

 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
 设有半径为3km的圆形村落,A、B两人同时从村落中心出发.B一直向北直行;A先向东直行,出村后一段时间,改变前进方向,沿着与村落边界相切的直线朝B所在的方向前进.
设有半径为3km的圆形村落,A、B两人同时从村落中心出发.B一直向北直行;A先向东直行,出村后一段时间,改变前进方向,沿着与村落边界相切的直线朝B所在的方向前进.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 设有半径为3km的圆形村落,A、B两人同时从村落中心出发.B一直向北直行;A先向东直行,出村后一段时间,改变前进方向,沿着与村落边界相切的直线朝B所在的方向前进.
设有半径为3km的圆形村落,A、B两人同时从村落中心出发.B一直向北直行;A先向东直行,出村后一段时间,改变前进方向,沿着与村落边界相切的直线朝B所在的方向前进.查看答案和解析>>
科目:高中数学 来源:2011-2012学年广东省肇庆市封开县南丰中学高三数学复习模块测试卷A (必修2)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com