
【题目】已知向量 ![]() =(x,﹣1),
=(x,﹣1), ![]() =(x﹣2,3),
=(x﹣2,3), ![]() =(1﹣2x,6).
=(1﹣2x,6).
(1)若 ![]() ⊥(2
⊥(2 ![]() +
+ ![]() ),求|
),求| ![]() |;
|;
(2)若 ![]()
![]() <0,求x的取值范围.
<0,求x的取值范围.
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在
是定义在![]() 上的偶函数,且当
上的偶函数,且当![]() 时,
时,![]() .
.

(1)已画出函数![]() 在
在![]() 轴左侧的图像,如图所示,请补出完整函数
轴左侧的图像,如图所示,请补出完整函数![]() 的图像,并根据图像写出函数
的图像,并根据图像写出函数![]() 的增区间;
的增区间;
⑵写出函数![]() 的解析式和值域.
的解析式和值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将两块三角板按图甲方式拼好,其中![]() ,
, ![]() ,
, ![]() ,
,
![]() ,现将三角板
,现将三角板![]() 沿
沿![]() 折起,使
折起,使![]() 在平面
在平面![]() 上的射影
上的射影![]() 恰好在
恰好在![]() 上,如图乙.
上,如图乙.
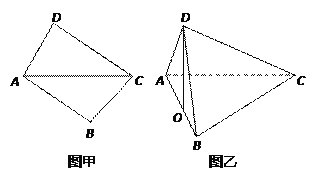
(1)求证: ![]() ;
;
(2)求证: ![]() 为线段
为线段![]() 中点;
中点;
(3)求二面角![]() 的大小的正弦值.
的大小的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x﹣2|﹣|2x+l|.
(I)求不等式f(x)≤x的解集;
(II )若不等式f(x)≥t2﹣t在x∈[﹣2,﹣1]时恒成立,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】锐角△ABC中,角A,B,C所对的边分别为a,b,c,且acosB+bcosA= ![]() csinC.
csinC.
(1)求cosC;
(2)若a=6,b=8,求边c的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(
=( ![]() sinx,﹣1),
sinx,﹣1), ![]() =(cosx,m),m∈R.
=(cosx,m),m∈R.
(1)若m= ![]() ,且
,且 ![]() ∥
∥ ![]() ,求
,求 ![]() 的值;
的值;
(2)已知函数f(x)=2( ![]() +
+ ![]() )
) ![]() ﹣2m2﹣1,若函数f(x)在[0,
﹣2m2﹣1,若函数f(x)在[0, ![]() ]上有零点,求m的取值范围.
]上有零点,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 的定义域为
的定义域为![]() ,若存在非零实数
,若存在非零实数![]() 满足对任意
满足对任意![]() ,均有
,均有![]() ,且
,且![]() ,则称
,则称![]() 为
为![]() 上的
上的![]() 高调函数. 如果定义域为
高调函数. 如果定义域为![]() 的函数
的函数![]() 是奇函数,当
是奇函数,当![]() 时,
时,![]() ,且
,且![]() 为
为![]() 上的8高调函数,那么实数
上的8高调函数,那么实数![]() 的取值范围为____.
的取值范围为____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一个半径为1的半球材料中截取两个高度均为![]() 的圆柱,其轴截面如图所示.设两个圆柱体积之和为
的圆柱,其轴截面如图所示.设两个圆柱体积之和为![]() .
.

(1)求![]() 的表达式,并写出
的表达式,并写出![]() 的取值范围;
的取值范围;
(2)求两个圆柱体积之和![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com