
【题目】
已知函数f(x)=![]() ,其中a>0.
,其中a>0.
(Ⅰ)若a=1,求曲线y=f(x)在点(2,f(2))处的切线方程;
(Ⅱ)若在区间![]() 上,f(x)>0恒成立,求a的取值范围.
上,f(x)>0恒成立,求a的取值范围.
【答案】(Ⅰ)y=6x-9(Ⅱ)0<a<5
【解析】
试题(1)利用导数求切线斜率即可;
(2)在区间![]() 上,
上,![]() 恒成立
恒成立![]() 恒成立,令
恒成立,令![]() ,解得
,解得![]() 或
或![]() ,以下分两种情况
,以下分两种情况![]() ,
,![]() 讨论,分类求出函数最大值即可.
讨论,分类求出函数最大值即可.
试题解析:(1)当a=1时,f(x)=x3-x2+1,f(2)=3;f' (x)=3x2-3x, f' (2)=6.
所以曲线y=f(x) 在点(2,f(2))处的切线方程y-3=6(x-2),即y=6x-9.
(2)f' (x)=3ax2-3x=3x(ax-1),令f' (x)=0,解得x=0或x=.
以下分两种情况讨论:
①若0<a≤2,则≥,当x变化时,f' (x),f(x)的变化情况如下表:
x | (-,0) | 0 | (0,) |
f' (x) | + | 0 | - |
f(x) | 递增 | 极大值 | 递减 |
当x[-,]上,f(x)>0等价于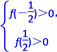 ,即
,即 解不等式组得-5<a<5.因此0<a≤2.
解不等式组得-5<a<5.因此0<a≤2.
②若a>2,则0<<,当x变化时,f' (x),f(x)的变化情况如下表:
X | (-,0) | 0 | (0,) | (,) | |
f' (x) | + | 0 | - | 0 | + |
f'(x) | 递增 | 极大值 | 递减 | 极小值 | 递增 |
当x[-,]上,f(x)>0等价于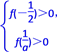 ,即
,即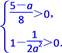 解不等式组得
解不等式组得![]() <a<5,或a<-
<a<5,或a<-![]() .因此2<a<5. 综合①和②,可知a的取值范围为0<a<5.
.因此2<a<5. 综合①和②,可知a的取值范围为0<a<5.


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在![]() 轴上,左顶点为
轴上,左顶点为![]() ,左焦点为
,左焦点为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,直线
上,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点,直线
两点,直线![]() ,
, ![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,
, ![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)以![]() 为直径的圆是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
为直径的圆是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年是五四运动100周年.五四运动以来的100年,是中国青年一代又一代接续奋斗、凯歌前行的100年,是中口青年用青春之我创造青春之中国、青春之民族的100年.为继承和发扬五四精神在青年节到来之际,学校组织“五四运动100周年”知识竞赛,竞赛的一个环节由10道题目组成,其中6道A类题、4道B类题,参赛者需从10道题目中随机抽取3道作答,现有甲同学参加该环节的比赛.
(1)求甲同学至少抽到2道B类题的概率;
(2)若甲同学答对每道A类题的概率都是![]() ,答对每道B类题的概率都是
,答对每道B类题的概率都是![]() ,且各题答对与否相互独立.现已知甲同学恰好抽中2道A类题和1道B类题,用X表示甲同学答对题目的个数,求随机变量X的分布列和数学期望.
,且各题答对与否相互独立.现已知甲同学恰好抽中2道A类题和1道B类题,用X表示甲同学答对题目的个数,求随机变量X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两支篮球队赛季总决赛采用7场4胜制,每场必须分出胜负,场与场之间互不影响,只要有一队获胜4场就结束比赛.现已比赛了4场,且甲篮球队胜3场.已知甲球队第5,6场获胜的概率均为![]() ,但由于体力原因,第7场获胜的概率为
,但由于体力原因,第7场获胜的概率为![]() .
.
(1)求甲队分别以![]() ,
,![]() 获胜的概率;
获胜的概率;
(2)设![]() 表示决出冠军时比赛的场数,求
表示决出冠军时比赛的场数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国南北朝数学家何承天发明的“调日法”是程序化寻求精确分数来表示数值的算法,其理论依据是:设实数![]() 的不足近似值和过剩近似值分别为
的不足近似值和过剩近似值分别为![]() 和
和![]() ,则
,则![]() 是
是![]() 的更为精确的不足近似值或过剩近似值.我们知道
的更为精确的不足近似值或过剩近似值.我们知道![]() ,若令
,若令![]() ,则第一次用“调日法”后得
,则第一次用“调日法”后得![]() 是
是![]() 的更为精确的过剩近似值,即
的更为精确的过剩近似值,即![]() ,若每次都取最简分数,那么第四次用“调日法”后可得
,若每次都取最简分数,那么第四次用“调日法”后可得![]() 的近似分数为( )
的近似分数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
已知函数![]()
![]() 有极值,且函数
有极值,且函数![]() 的极值点是
的极值点是![]() 的极值点,其中
的极值点,其中![]() 是自然对数的底数.(极值点是指函数取得极值时对应的自变量的值)
是自然对数的底数.(极值点是指函数取得极值时对应的自变量的值)
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)当![]() 时,若函数
时,若函数![]() 的最小值为
的最小值为![]() ,证明:
,证明: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有一块半圆形的空地,政府计划在空地上建一个矩形的市民活动广场ABCD及矩形的停车场EFGH,剩余的地方进行绿化,其中半圆的圆心为O,半径为r,矩形的一边AB在直径上,点C,D,G,H在圆周上,E,F在边CD上,且∠BOG=60°,设∠BOC=![]() .
.

(1)记市民活动广场及停车场的占地总面积为![]() ,求
,求![]() 的表达式;
的表达式;
(2)当cos![]() 为何值时,可使市民活动广场及停车场的占地总面积最大.
为何值时,可使市民活动广场及停车场的占地总面积最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com