
A.回归直线必过样本中心点 |
| B.回归直线就是散点图中经过样本数据点最多的那条直线 |
| C.从独立性检验可知有99%的把握认为吸烟与患肺病有关系时,我们说某人吸烟,那么此人有99%的可能患有肺病 |
| D.某车间包装一种产品,在自动包装的传送带上每隔30分钟抽取一件产品作检验,这种抽样为简单随机抽样 |
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案科目:高中数学 来源:不详 题型:单选题
| A.3,2 | B.28,32 | C.23,23 | D.8,2 |

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.14辆,21辆,12辆 | B.7辆,30辆,10辆 |
| C.10辆,20辆,17辆 | D.8辆,21辆,18辆 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 频率分布表
频率分布表| 分组 | 频数 | 频率 | 频率/组距 |
| (10,20] | 2 | 0.10 | 0.010 |
| (20,30] | 3 | 0.15 | 0.015 |
| (30,40] | 4 | 0.20 | 0.020 |
| (40,50] | a | b | 0.025 |
| (50,60] | 4 | 0.20 | 0 .020 .020 |
(60, 70] 70] | 2 | 0.10 | 0.010 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
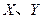 (单位:
(单位: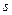 ),其分布如下:
),其分布如下: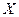 | 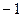 | 0 | 1 |
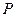 | 0.1 | 0.8 | 0.1 |
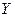 | 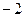 | 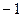 | 0 | 1 | 2 |
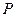 | 0.1 | 0.2 | 0.4 | 0.2 | 0.1 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 =" " 。若要从身高在[120,130﹚,[130,140﹚,[140,150]三组内的学生中,用分层抽样的方法选取18人参加一项活动,则从身高在[140,150]内的学生中选取的人数应为 .
=" " 。若要从身高在[120,130﹚,[130,140﹚,[140,150]三组内的学生中,用分层抽样的方法选取18人参加一项活动,则从身高在[140,150]内的学生中选取的人数应为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com