
分析 (1)利用已知是递推公式推导$\frac{{a}_{n+1}}{1-{a}_{n+1}}:\frac{{a}_{n}}{1-{a}_{n}}$为定值即可;
(2)由(1)的结论得到数列{$\frac{n}{{a}_{n}}$}的通项公式,利用错位相减法求和.
解答 证明:(1)由an+1an+an+1=2an,得到${a}_{n+1}=\frac{2{a}_{n}}{1+{a}_{n}}$,
$\frac{{a}_{n+1}}{1-{a}_{n+1}}:\frac{{a}_{n}}{1-{a}_{n}}$=$\frac{\frac{2{a}_{n}}{1+{a}_{n}}}{1-\frac{2{a}_{n}}{{a}_{n}+1}}:\frac{{a}_{n}}{1-{a}_{n}}$=$\frac{2{a}_{n}}{1-{a}_{n}}:\frac{{a}_{n}}{1-{a}_{n}}$=2,
所以{$\frac{{a}_{n}}{1-{a}_{n}}$}的等比数列;
(2)由(1)得到$\frac{{a}_{1}}{1-{a}_{1}}$=2,所以$\frac{{a}_{n}}{1-{a}_{n}}$=2×2n-1=2n,
所以数列{$\frac{n}{{a}_{n}}$}的通项公式$\frac{n}{{a}_{n}}=\frac{n}{{2}^{n}}$,
设它的前n项和为S=$\frac{1}{2}+\frac{2}{{2}^{2}}+\frac{3}{{2}^{3}}+…+\frac{n}{{2}^{n}}$,
$\frac{1}{2}$S=$\frac{1}{{2}^{2}}+\frac{2}{{2}^{3}}+\frac{3}{{2}^{4}}+…+\frac{n-1}{{2}^{n}}+\frac{n}{{2}^{n+1}}$,
两式相减得$\frac{1}{2}$S=$\frac{1}{2}+\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}+…+\frac{1}{{2}^{n}}-\frac{n}{{2}^{n+1}}$=$\frac{\frac{1}{2}(1-\frac{1}{{2}^{n}})}{1-\frac{1}{2}}-\frac{n}{{2}^{n+1}}$,
所以S=2-$\frac{n+2}{{2}^{n}}$.
所以数列{$\frac{n}{{a}_{n}}$}的前n项和为2-$\frac{n+2}{{2}^{n}}$.
点评 本题考查了数列的递推公式、等比数列的定义运用以及错位相减法求数列的前n项和;属于中档题.


科目:高中数学 来源: 题型:解答题
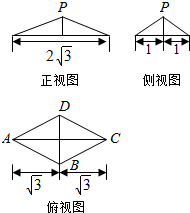 已知四棱锥P-ABCD的三视图如图所示,其中俯视图是菱形,正视图和侧视图都是等腰三角形,已知M为BC上一点,且BM=$\frac{1}{2}$,PA⊥PM.
已知四棱锥P-ABCD的三视图如图所示,其中俯视图是菱形,正视图和侧视图都是等腰三角形,已知M为BC上一点,且BM=$\frac{1}{2}$,PA⊥PM.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com