
【题目】已知定义在[﹣2,2]上的函数y=f(x)和y=g(x),其图象如图所示:给出下列四个命题:
①方程f[g(x)]=0有且仅有6个根 ②方程g[f(x)]=0有且仅有3个根
③方程f[f(x)]=0有且仅有5个根 ④方程g[g(x)]=0有且仅有4个根
其中正确命题的序号( )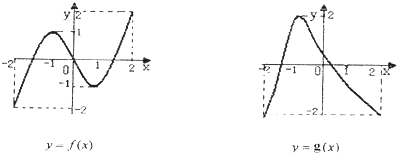
A.①②③
B.②③④
C.①②④
D.①③④
【答案】D
【解析】解:由图象可得﹣2≤g(x)≤2,﹣2≤f(x)≤2,①由于满足方程f[g(x)]=0 的g(x)有三个不同值,由于每个值g(x)对应了2个x值,
故满足f[g(x)]=0的x值有6个,即方程f[g(x)]=0有且仅有6个根,故①正确.
②由于满足方程g[f(x)]=0的f(x)有2个不同的值,从图中可知,每一个值f(x),
一个f(x)的值在(﹣2,﹣1)上,令一个f(x)的值在(0,1)上.
当f(x)的值在(﹣2,﹣1)上时,原方程有一个解;f(x)的值在(0,1)上,原方程有3个解.
故满足方程g[f(x)]=0的x值有4个,故②不正确.
③由于满足方程f[f(x)]=0的f(x)有3个不同的值,从图中可知,一个f(x)等于0,
一个f(x)∈(﹣2,﹣1),一个f(x)∈(1,2).
而当f(x)=0对应了3个不同的x值;当f(x)∈(﹣2,﹣1)时,只对应一个x值;
当f(x)∈(1,2)时,也只对应一个x值.
故满足方程f[f(x)]=0的x值共有5个,故③正确.
④由于满足方程g[g(x)]=0 的g(x)值有2个,而结合图象可得,每个g(x)值对应2个不同的x值,
故满足方程g[g(x)]=0 的x值有4个,即方程g[g(x)]=0有且仅有4个根,故④正确.
故选 D.


科目:高中数学 来源: 题型:
【题目】已知直线l:y=4x和点P(6,4),点A为第一象限内的点且在直线l上,直线PA交x轴正半轴于点B,
(1)当OP⊥AB时,求AB所在直线的直线方程;
(2)求△OAB面积的最小值,并求当△OAB面积取最小值时的B的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在英国的某一娱乐节目中,有一种过关游戏,规则如下:转动图中转盘(一个圆盘四等分,在每块区域内分别标有数字1,2,3,4),由转盘停止时指针所指数字决定是否过关.在闯![]() 关时,转
关时,转![]() 次,当次转得数字之和大于
次,当次转得数字之和大于![]() 时,算闯关成功,并继续闯关,否则停止闯关,闯过第一关能获得10欧元,之后每多闯一关,奖金翻倍,假设每个参与者都会持续闯关到不能过关为止,并且转盘每次转出结果相互独立.
时,算闯关成功,并继续闯关,否则停止闯关,闯过第一关能获得10欧元,之后每多闯一关,奖金翻倍,假设每个参与者都会持续闯关到不能过关为止,并且转盘每次转出结果相互独立.
(1)求某人参加一次游戏,恰好获得10欧元的概率;
(2)某人参加一次游戏,获得奖金![]() 欧元,求
欧元,求![]() 的概率分布和数学期望.
的概率分布和数学期望.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于三次函数f(x)=ax3+bx2+cx+d(a≠0),给出定义:设f′(x)是函数y=f(x)的导数,f″(x)是f′(x)的导数,若方程f″(x)=0有实数解x0,则称点(x0,f(x0))为函数y=f(x)的“拐点”.某同学经过探究发现:任何一个三次函数都有对称中心,且“拐点”就是对称中心.若![]() ,请你根据这一发现判断函数
,请你根据这一发现判断函数![]() 的对称中心为( )
的对称中心为( )
A. (![]() ,1) B. (-
,1) B. (-![]() ,1) C. (
,1) C. (![]() ,-1) D. (-
,-1) D. (-![]() ,-1)
,-1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=kax﹣a﹣x(a>0且a≠1)是定义域为R的奇函数.
(1)若f(1)>0,试求不等式f(x2+2x)+f(x﹣4)>0的解集;
(2)若f(1)= ![]() ,且g(x)=a2x+a﹣2x﹣2mf(x)在[1,+∞)上的最小值为﹣2,求m的值.
,且g(x)=a2x+a﹣2x﹣2mf(x)在[1,+∞)上的最小值为﹣2,求m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分10分)选修4-5:不等式选讲
已知函数f(x)=log2(|x+1|+|x﹣2|﹣m).
(1)当m=7时,求函数f(x)的定义域;
(2)若关于x的不等式f(x)≥2的解集是R,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:x∈[1,2],x2≥a;命题q:x∈R,x2+2ax+2﹣a=0,若命题p∧q是真命题,则实数a的取值范围是( )
A.a≤﹣2或a=1
B.a≤﹣2或1≤a≤2
C.a≥1
D.﹣2≤a≤1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com