
【题目】如图,有一直角墙角,两边的长度足够长,若P处有一棵树与两墙的距离分别是4m和am(0<a<12),不考虑树的粗细.现用16m长的篱笆,借助墙角围成一个矩形花圃ABCD.设此矩形花圃的最大面积为u,若将这棵树围在矩形花圃内,则函数u=f(a)(单位m2)的图象大致是( ) 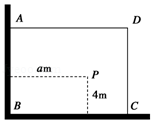
A.
B.
C.
D.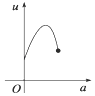
科目:高中数学 来源: 题型:
【题目】已知圆C:![]() ,直线
,直线![]() :
:![]() .
.
(1)若直线![]() 被圆C截得的弦长为
被圆C截得的弦长为![]() ,求实数
,求实数![]() 的值;
的值;
(2)当t =1时,由直线![]() 上的动点P引圆C的两条切线,若切点分别为A,B,则直线AB是否恒过一个定点?若存在,求出该定点的坐标;若不存在,请说明理由.
上的动点P引圆C的两条切线,若切点分别为A,B,则直线AB是否恒过一个定点?若存在,求出该定点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了分析本校高中生的性别与是否喜欢数学之间的关系,在高中生中随机地抽取了90名学生调查,得到了如下列联表:
喜欢数学 | 不喜欢数学 | 总计 | |
男 | 30 | ① | 45 |
女 | ② | 25 | 45 |
总计 | ③ | ④ | 90 |
(1)求①②③④处分别对应的值;
(2)能有多大把握认为“高中生的性别与喜欢数学”有关?
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记![]() 表示大于
表示大于![]() 的整数
的整数![]() 的十位数,例如
的十位数,例如![]() ,
,![]() .已知
.已知![]() ,
,![]() ,
,![]() 都是大于
都是大于![]() 的互不相等的整数,现有如下
的互不相等的整数,现有如下![]() 个命题:
个命题:
①若![]() ,则
,则![]() ;②
;②![]() ,
,![]() 且
且![]() ;
;
③若![]() 是质数,则
是质数,则![]() 也是质数;④若
也是质数;④若![]() ,
,![]() ,
,![]() 成等差数列,则
成等差数列,则![]() ,
,![]() ,
,![]() 可能成等比数列.
可能成等比数列.
其中所有的真命题为( )
A. ② B. ③④ C. ①②④ D. ①②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是菱形,
是菱形,![]() ,
,![]() 为等边三角形,
为等边三角形,![]() 是线段
是线段![]() 上的一点,且
上的一点,且![]() 平面
平面![]() .
.

(1)求证:![]() 为
为![]() 的中点;
的中点;
(2)若![]() 为
为![]() 的中点,连接
的中点,连接![]() ,
,![]() ,
,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知从圆C:(x+1)2+(y﹣2)2=2外一点P(x1 , y1)向该圆引一条切线,切点为M,O为坐标原点,且有|PM|=|PO|,则当|PM|取最小值时点P的坐标为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在△ABC中,AB的中点为O,且OA=1,点D在AB的延长线上,且 ![]() .固定边AB,在平面内移动顶点C,使得圆M与边BC,边AC的延长线相切,并始终与AB的延长线相切于点D,记顶点C的轨迹为曲线Γ.以AB所在直线为x轴,O为坐标原点如图所示建立平面直角坐标系.
.固定边AB,在平面内移动顶点C,使得圆M与边BC,边AC的延长线相切,并始终与AB的延长线相切于点D,记顶点C的轨迹为曲线Γ.以AB所在直线为x轴,O为坐标原点如图所示建立平面直角坐标系. 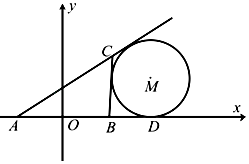
(Ⅰ)求曲线Γ的方程;
(Ⅱ)设动直线l交曲线Γ于E、F两点,且以EF为直径的圆经过点O,求△OEF面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究某班学生的脚长x(单位:厘米)和身高y(单位:厘米)的关系,从该班随机抽取10名学生,根据测量数据的散点图可以看出y与x之间有线性相关关系,设其回归直线方程为 ![]() =
= ![]() x+
x+ ![]() ,已知
,已知 ![]() xi=225,
xi=225, ![]() yi=1600,
yi=1600, ![]() =4,该班某学生的脚长为24,据此估计其身高为( )
=4,该班某学生的脚长为24,据此估计其身高为( )
A.160
B.163
C.166
D.170
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com