
如图,在四棱锥 中,底面
中,底面 为矩形,
为矩形, 底面
底面 ,
, 、
、 分别是
分别是 、
、 中点.
中点.

(1)求证: 平面
平面 ;
;
(2)求证: .
.
(1)参考解析;(2)参考解析
【解析】
试题分析:(1)要证直线与平面平行,根据直线与平面平行的判定定理,需要在平面内找一条直线与已知直线平行,由于本小题中点较多,所以想到作出四边形AMNQ.通过判定平行四边形,然后再用平行四边形的性质得到所需要的两直线平行,这种方法也是在证明直线与平面平行时的常用的方法.
(2)直线与直线垂直的证明根据判断定理,一般需要转化为证明直线与平面的垂直.这题是根据第一步的结论证明AB与平面PAD垂直,从而可得结论.

试题解析:证明:(1)取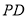 中点
中点 ,连结
,连结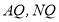 .
.
因为  是
是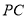 中点,
中点,
所以  .
.
又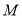 是
是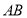 中点,
中点, ,
,
所以 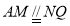 ,
,
四边形 是平行四边形.所以
是平行四边形.所以 .因为
.因为 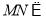 平面
平面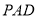 ,
,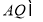 平面
平面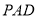 ,
,
所以 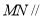 平面
平面 . 7分
. 7分
(2)因为 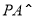 平面
平面 ,所以
,所以  .
.
又 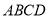 是矩形,
是矩形,
所以 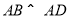 .
.
所以 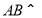 平面
平面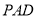 ,
,
所以  .又
.又 ,
,
所以 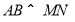 .
.
考点:1.直线与平面平行的判断定理.2.直线与直线垂直的判断方法.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源:2015届北京海淀区高二上学期期末考试理科数学试卷(解析版) 题型:选择题
已知命题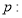 椭圆的离心率
椭圆的离心率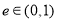 ,命题
,命题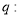 与抛物线只有一个公共点的直线是此抛物线的切线,那么( )
与抛物线只有一个公共点的直线是此抛物线的切线,那么( )
(A) 是真命题 (B)
是真命题 (B) 是真命题
是真命题
(C) 是真命题 (D)
是真命题 (D)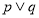 是假命题
是假命题
查看答案和解析>>
科目:高中数学 来源:2015届北京市西城区高二第一学期期末理科数学试卷(解析版) 题型:解答题
已知 为椭圆
为椭圆 上的三个点,
上的三个点, 为坐标原点.
为坐标原点.
(1)若 所在的直线方程为
所在的直线方程为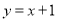 ,求
,求 的长;
的长;
(2)设 为线段
为线段 上一点,且
上一点,且 ,当
,当 中点恰为点
中点恰为点 时,判断
时,判断 的面积是否为常数,并说明理由.
的面积是否为常数,并说明理由.
查看答案和解析>>
科目:高中数学 来源:2015届北京市西城区高二第一学期期末理科数学试卷(解析版) 题型:选择题
“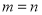 ”是“方程
”是“方程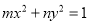 表示圆”的 ( )
表示圆”的 ( )
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2015届北京市西城区高二第一学期期末文科数学试卷(解析版) 题型:选择题
已知椭圆 ,
, 为坐标原点.若
为坐标原点.若 为椭圆上一点,且在
为椭圆上一点,且在 轴右侧,
轴右侧, 为
为 轴上一点,
轴上一点, ,则点
,则点 横坐标的最小值为( )
横坐标的最小值为( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:高中数学 来源:2015届北京东城(南片)高二上学期期末考试文数学试卷(解析版) 题型:选择题
甲、乙、丙三名毕业生参加某公司人力资源部安排的面试,三人依次进行,每次一人,其中甲、乙两人相邻的概率为
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com