
(本小题满分13分)设数列 的前
的前 项和为
项和为 .已知
.已知 ,
, ,
, .
.
(1)写出 的值,并求数列
的值,并求数列 的通项公式;
的通项公式;
(2)记 为数列
为数列 的前
的前 项和,求
项和,求 ;
;
(3)若数列 满足
满足 ,
, ,求数列
,求数列 的通项公式.
的通项公式.
(1) ;(2)
;(2) ;(3)
;(3)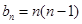 。
。
解析试题分析:(Ⅰ)由已知得, ,
, . …………………2分
. …………………2分
由题意, ,则当
,则当 时,
时, .
.
两式相减,得 (
( ). ………………………3分
). ………………………3分
又因为 ,
, ,
, ,
,
所以数列 是以首项为
是以首项为 ,公比为
,公比为 的等比数列,
的等比数列,
所以数列 的通项公式是
的通项公式是 (
( ). ………………………………4分
). ………………………………4分
(Ⅱ)因为 ,
,
所以 , ……………………5分
, ……………………5分
两式相减得, , ………7分
, ………7分
整理得, (
( ). ………………………………8分
). ………………………………8分
(Ⅲ) 当 时,依题意得
时,依题意得 ,
, ,… ,
,… ,  .
.
相加得, . …………………11分
. …………………11分
依题意 .
.
因为 ,所以
,所以 (
( ).
).
显然当 时,符合.
时,符合.
所以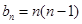 (
( ). …………………13分
). …………………13分
考点:数列通项公式的求法。错位相减法求数列前n项和。
点评:我们要熟练掌握求数列通项公式的方法。公式法是求数列通项公式的基本方法之一,常用的公式有:等差数列的通项公式、等比数列的通项公式及公式 。此题的第一问求数列的通项公式就是用公式
。此题的第一问求数列的通项公式就是用公式 ,用此公式要注意讨论
,用此公式要注意讨论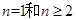 的情况。
的情况。


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:高中数学 来源: 题型:解答题
(本题满分13分)
设数列 为单调递增的等差数列,
为单调递增的等差数列, ,且
,且 依次成等比数列.
依次成等比数列.
(Ⅰ)求数列 的通项公式
的通项公式 ;
;
(Ⅱ)若 ,求数列
,求数列 的前
的前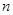 项和
项和 ;
;
(Ⅲ)若 ,求数列
,求数列 的前
的前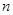 项和
项和 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com