
【题目】已知函数![]() .
.
(1)指出函数![]() 的基本性质:定义域,奇偶性,单调性,值域(结论不需证明),并作出函数
的基本性质:定义域,奇偶性,单调性,值域(结论不需证明),并作出函数![]() 的图象;
的图象;
(2)若关于![]() 的不等式
的不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若关于![]() 的方程
的方程![]() 恰有
恰有![]() 个不同的实数解,求实数
个不同的实数解,求实数![]() 的取值范围.
的取值范围.
【答案】(1)定义域:![]() ,
,![]() 是偶函数,在区间
是偶函数,在区间![]() 和
和![]() 上单调递增,在区间
上单调递增,在区间![]() 和
和![]() 上单调递减,值域为
上单调递减,值域为![]() ,作图见解析;(2)
,作图见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)将函数![]() 表示为分段函数,利用基本初等函数的基本性质可得出函数
表示为分段函数,利用基本初等函数的基本性质可得出函数![]() 的定义域、奇偶性、单调性和值域,并结合解析式作出该函数的图象;
的定义域、奇偶性、单调性和值域,并结合解析式作出该函数的图象;
(2)令![]() ,可得出不等式
,可得出不等式![]() 在
在![]() 恒成立,然后利用参变量分离法得出
恒成立,然后利用参变量分离法得出![]() ,求出函数
,求出函数![]() 的最大值,即可得出实数
的最大值,即可得出实数![]() 的取值范围;
的取值范围;
(3)令![]() ,结合题意可得知关于
,结合题意可得知关于![]() 的方程
的方程![]() 的两根
的两根![]() ,
,![]() ,然后利用二次函数的零点分布列出关于
,然后利用二次函数的零点分布列出关于![]() 、
、![]() 的不等式组,即可求出实数
的不等式组,即可求出实数![]() 的取值范围.
的取值范围.
(1)![]() ,
,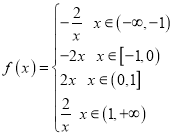 ,函数
,函数![]() 是偶函数,
是偶函数,
在区间![]() 和
和![]() 上单调递增,在区间
上单调递增,在区间![]() 和
和![]() 上单调递减,
上单调递减,
函数![]() 的最大值是
的最大值是![]() ,无最小值,值域为
,无最小值,值域为![]() .
.
作图如下:
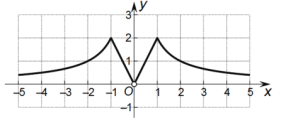
(2)因为关于![]() 的不等式
的不等式![]() 恒成立,
恒成立,
令![]() ,则
,则![]() ,即不等式
,即不等式![]() 在
在![]() 恒成立.
恒成立.
当![]() 时,因为
时,因为![]() ,所以
,所以![]() .
.
又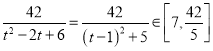 ,所以
,所以![]() ;
;
(3)关于![]() 的方程
的方程![]()
![]() 恰有
恰有![]() 个不同的实数解即
个不同的实数解即![]() 有
有![]() 个不同的解,如下图所示:
个不同的解,如下图所示:
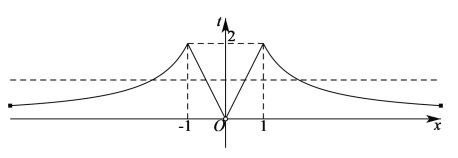
当![]() 时,方程
时,方程![]() 有四个根;当
有四个根;当![]() 时,方程
时,方程![]() 有两个根;
有两个根;
当![]() 或
或![]() 时, 方程
时, 方程![]() 无解.
无解.
设方程![]() 的两根分别为
的两根分别为![]() 、
、![]() ,则
,则![]() ,
,![]() .
.
令![]() ,则
,则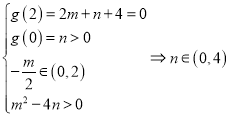 .
.
因此,实数![]() 的取值范围是
的取值范围是![]() .
.


 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:
【题目】在人群流量较大的街道,有一中年人吆喝“送钱”,只见他手拿一黑色小布袋,袋中有3只黄色、3只白色的乒乓球(其体积、质地完成相同),旁边立着一块小黑板写道:
摸球方法:从袋中随机摸出3个球,若摸得同一颜色的3个球,摊主送给摸球者5元钱;若摸得非同一颜色的3个球,摸球者付给摊主1元钱.
(1)摸出的3个球为白球的概率是多少?
(2)摸出的3个球为2个黄球1个白球的概率是多少?
(3)假定一天中有100人次摸奖,试从概率的角度估算一下这个摊主一个月(按30天计)能赚多少钱?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)的定义域为D={x|x≠0},且满足对于任意x1,x2∈D,有f(x1·x2)=f(x1)+f(x2).
(1)求f(1)的值;
(2)判断f(x)的奇偶性并证明你的结论;
(3)如果f(4)=1,f(x-1)<2,且f(x)在(0,+∞)上是增函数,求x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是正四面体的平面展开图,![]() 分别是
分别是![]() 的中点,在这个正四面体中:①
的中点,在这个正四面体中:①![]() 与
与![]() 平行;②
平行;②![]() 与
与![]() 为异面直线;③
为异面直线;③![]() 与
与![]() 成60°角;④
成60°角;④![]() 与
与![]() 垂直.以上四个命题中,正确命题的个数是( )
垂直.以上四个命题中,正确命题的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,海中一小岛C周围![]() nmile内有暗礁,货轮由西向东航行至A处测得小岛C位于北偏东75°方向上,航行8nmile后,于B处测得小岛C在北偏东60°方向上.
nmile内有暗礁,货轮由西向东航行至A处测得小岛C位于北偏东75°方向上,航行8nmile后,于B处测得小岛C在北偏东60°方向上.

(1)如果这艘货轮不改变航向继续前进,有没有触礁的危险?请说明理由.
(2)如果有触礁的危险,这艘货轮在B处改变航向为南偏东α°(α>0)方向航行,顺利绕过暗礁,求a的最大值.(附:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρsin2α﹣4cosα=0.已知直线l的参数方程为![]() (
(![]() 为参数),点M的直角坐标为
为参数),点M的直角坐标为![]() .
.
(1)求直线l和曲线C的普通方程;
(2)设直线l与曲线C交于A,B两点,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com