
【题目】若 ![]() (tanx+sinx)﹣
(tanx+sinx)﹣ ![]() |tanx﹣sinx|﹣k≥0在x∈[
|tanx﹣sinx|﹣k≥0在x∈[ ![]() ,
, ![]() π]恒成立,则k的取值范围是 .
π]恒成立,则k的取值范围是 .
【答案】(﹣∞,﹣1]
【解析】解:∵tanx﹣sinx=sinx( ![]() ﹣1),x∈[
﹣1),x∈[ ![]() ], ∴cosx<0,
], ∴cosx<0,
①当x∈[ ![]() )时,sinx>0,
)时,sinx>0,
∴tanx﹣sinx=sinx( ![]() ﹣1)<0,
﹣1)<0,
∴ ![]() (tanx+sinx)﹣
(tanx+sinx)﹣ ![]() |tanx﹣sinx|﹣k=tanx﹣k≥0,
|tanx﹣sinx|﹣k=tanx﹣k≥0,
∴k≤tanx,
∵x∈[ ![]() ),
),
∴tanx的最小值为tan ![]() =﹣1,
=﹣1,
∴k≤﹣1.
②当x∈[π, ![]() ]时,sinx≤0,
]时,sinx≤0,
∴tanx﹣sinx=sinx( ![]() ﹣1)>0,
﹣1)>0,
∴ ![]() (tanx+sinx)﹣
(tanx+sinx)﹣ ![]() |tanx﹣sinx|﹣k=sinx﹣k≥0,
|tanx﹣sinx|﹣k=sinx﹣k≥0,
∴k≤sinx,
∵x∈[ ![]() ),
),
∴sinx的最小值为sin ![]() =﹣
=﹣ ![]() ,
,
∴k≤﹣ ![]() .
.
综上所述,k≤﹣1.
∴k的取值范围是(﹣∞,﹣1].
所以答案是:(﹣∞,﹣1].


 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2x﹣8,g(x)=2x2﹣5x﹣18
(1)求不等式g(x)<0的解集
(2)若对一切x>2,均有f(x)≥(m+2)x﹣m﹣15成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在海岸A处,发现北偏东45°方向,距A处( ![]() ﹣1)海里的B处有一艘走私船,在A处北偏西75°方向,距A处2海里的C处的缉私船奉命以10
﹣1)海里的B处有一艘走私船,在A处北偏西75°方向,距A处2海里的C处的缉私船奉命以10 ![]() 海里/小时的速度追截走私船,此时走私船正以10海里/小时的速度从B处向北偏东30°的方向逃窜,问缉私船沿什么方向能最快追上走私船,并求出所需要的时间.
海里/小时的速度追截走私船,此时走私船正以10海里/小时的速度从B处向北偏东30°的方向逃窜,问缉私船沿什么方向能最快追上走私船,并求出所需要的时间. 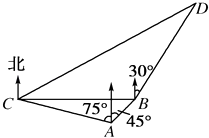
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(Ⅰ)求图中![]() 的值;
的值;
(Ⅱ)根据频率分布直方图,估计这100名学生语文成绩的平均分;
(Ⅲ)若这100名学生语文成绩某些分数段的人数(![]() )与数学成绩相应分数段的人数(
)与数学成绩相应分数段的人数(![]() )之比如表所示,求数学成绩在
)之比如表所示,求数学成绩在![]() 之外的人数.
之外的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱ABCD﹣A1B1C1D1中,已知DC=DD1=2AD=2AB,AD⊥DC,AB∥DC. 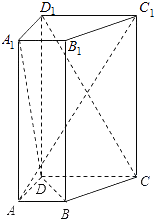
(1)求证:D1C⊥AC1;
(2)设E是DC上一点,试确定E的位置,使D1E∥平面A1BD,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C的方程为:x2+y2﹣2mx﹣2y+4m﹣4=0,(m∈R).
(1)试求m的值,使圆C的面积最小;
(2)求与满足(1)中条件的圆C相切,且过点(1,﹣2)的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高二年级进行了百科知识大赛,为了了解高二年级900名同学的比赛情况,现在甲、乙两个班级各随机抽取了10名同学的成绩,比赛成绩满分为100分,80分以上可获得二等奖,90分以上可以获得一等奖,已知抽取的两个班学生的成绩(单位:分)数据的茎叶图如图1所示:

(1)比较两组数据的分散程度(只需要给出结论),并求出甲组数据的频率分布直方图如图2中所示的![]() 值;
值;
(2)现从两组数据中获奖的学生里分别随机抽取一人接受采访,求被抽中的甲班学生成绩高于乙班学生成绩的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点.
两点.
(Ⅰ)若直线![]() 过焦点
过焦点![]() ,且与圆
,且与圆![]() 交于
交于![]() (其中
(其中![]() 在
在![]() 轴同侧),求证:
轴同侧),求证: ![]() 是定值;
是定值;
(Ⅱ)设抛物线![]() 在
在![]() 和
和![]() 点的切线交于点
点的切线交于点![]() ,试问:
,试问: ![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 为菱形?若存在,请说明理由并求此时直线
为菱形?若存在,请说明理由并求此时直线![]() 的斜率和点
的斜率和点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com