
����Ŀ����ͼ��ij��ˮ������Ҫ��һ��������ˮ������![]() �ijص�ˮƽ������ˮ�����ܵ���
�ijص�ˮƽ������ˮ�����ܵ���![]() ��
��![]() ��ֱ�Ƕ��㣩��������ˮ���ܵ�Խ������ˮ����Ч��Խ�ã����Ҫ��ܵ��Ľӿ�
��ֱ�Ƕ��㣩��������ˮ���ܵ�Խ������ˮ����Ч��Խ�ã����Ҫ��ܵ��Ľӿ�![]() ��
��![]() ���е㣬
���е㣬![]() �ֱ������߶�
�ֱ������߶�![]() �ϣ���֪
�ϣ���֪![]() �ף�
�ף�![]() �ף���
�ף���![]() ��
��
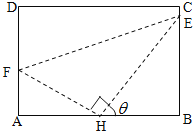
��1���Խ���ˮ�����ܵ��ij���![]() ��ʾΪ
��ʾΪ![]() �ĺ�������д��������
�ĺ�������д��������
��2����![]() �����ʱ�ܵ��ij���
�����ʱ�ܵ��ij���![]() ��
��
��3����![]() ȡ��ֵʱ����ˮ����Ч����ã��������ʱ�ܵ��ij��ȣ�
ȡ��ֵʱ����ˮ����Ч����ã��������ʱ�ܵ��ij��ȣ�
���𰸡�(1)![]() ��
��![]() ��(2)
��(2) ![]() �� (3)
�� (3)![]() ��
��![]() ʱ����ˮ����Ч����ã���ʱ�ܵ��ij���Ϊ
ʱ����ˮ����Ч����ã���ʱ�ܵ��ij���Ϊ![]() ��
��![]()
��������
![]() ����ֱ�������α�ʾ
����ֱ�������α�ʾ![]() ��
��![]() ��
��![]() �����ý����
�����ý����![]() ����ͬ�����Ǻ�����ϵ���
����ͬ�����Ǻ�����ϵ���![]() �����ý����
�����ý����![]() ����ͬ�����Ǻ�����ϵ��������ת��ΪһԪ���������ݵ����Եý��.
����ͬ�����Ǻ�����ϵ��������ת��ΪһԪ���������ݵ����Եý��.
�⣺![]() ��
��![]() ��
��![]() ��
��
����![]() ��
��![]() ��
��
����![]() ������
������![]() ������
������![]() ��
��![]() ��
��
![]() ��
��![]() ʱ��
ʱ��![]() ��
��
![]() ��
��![]() ��
��
![]() ����
����![]() ����
����![]() ��
��
����![]() ������
������![]() ������
������![]() ��
��
����![]() ��
��![]() �ϵ����ݼ���
�ϵ����ݼ���
���Ե�![]() ����
����![]() ��
��![]() ʱ��Lȡ�����ֵ
ʱ��Lȡ�����ֵ![]() ��
��![]()
�𣺵�![]() ��
��![]() ʱ����ˮ����Ч����ã���ʱ�ܵ��ij���Ϊ
ʱ����ˮ����Ч����ã���ʱ�ܵ��ij���Ϊ![]() ��
��![]()


 ��ĩ1�����ʽ���������ϵ�д�
��ĩ1�����ʽ���������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x��=|x��1|+![]() |x��3|
|x��3|
������ʽf��x����2�Ľ⼯��
����������ʽf��x����a��x+![]() ���Ľ⼯�ǿգ���ʵ��a��ȡֵ��Χ��
���Ľ⼯�ǿգ���ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��A,B������ѧ��ѧ����Ӳμӱ�������A��ѧ�Ƽ�3��������2��Ů����B��ѧ�Ƽ���3��������4��Ů������У�Ƽ���ѧ��һ��μӼ�ѵ�����ڼ�ѵ���Ա��ˮƽ�൱���ӲμӼ�ѵ�������������ȡ3�ˣ�Ů���������ȡ3����ɴ�����
��1����A��ѧ������1��ѧ����ѡ�����ӵĸ���.
��2��ij������ǰ���Ӵ����ӵ�6����Ա�������ȡ4�˲�������X��ʾ������������������X�÷ֲ��к���ѧ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() ��ͼ������ƽ��
��ͼ������ƽ��![]() ����λ���õ�����
����λ���õ�����![]() ��ͼ��������˵����ȷ���ǣ� ����
��ͼ��������˵����ȷ���ǣ� ����
A. ![]() B. ֱ��
B. ֱ��![]() ��
��![]() ��ͼ���һ���Գ���
��ͼ���һ���Գ���
C. ![]() ����С������Ϊ
����С������Ϊ![]() D.
D. ![]() Ϊ�溯��
Ϊ�溯��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������C1��y2=4mx��m��0��������x�ύ��F1 �� ����ΪF2����F1 �� F2Ϊ���㣬������e=![]() ����ԲC2��������C1��x���Ϸ��Ľ���ΪP���ӳ�PF2���������ڵ�Q��M��������C1��һ���㣬��M��P��Q֮���˶���
����ԲC2��������C1��x���Ϸ��Ľ���ΪP���ӳ�PF2���������ڵ�Q��M��������C1��һ���㣬��M��P��Q֮���˶���
��m=1ʱ������ԲC2�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
�� ![]() ��
��
��1����![]()
![]() ����
����![]() ��ż��������ʵ��
��ż��������ʵ��![]() ��ֵ��
��ֵ��
��2����![]() ������
������![]() ������
������![]() �ϵ�ֵ����
�ϵ�ֵ����
��3��������ʽ![]() ���������ʵ��
���������ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��������![]() �У�����ABCD�������Σ�AC��BD���ڵ�O��
�У�����ABCD�������Σ�AC��BD���ڵ�O��![]() ����ABCD��FΪBE���е㣬
����ABCD��FΪBE���е㣬![]() ��
��
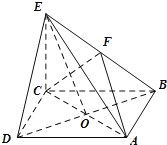
��1����֤��![]() ƽ��ACF��
ƽ��ACF��
��2����BE��ƽ��ACE�����ɽǵ�����ֵ��
��3�����߶�EO���Ƿ���ڵ�G��ʹCG![]() ƽ��BDE ?�����ڣ����EG��EO��ֵ���������ڣ���˵�����ɣ�
ƽ��BDE ?�����ڣ����EG��EO��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�����˿ͣ�ij�̳���ͨ������ҽ��ķ�ʽ��1000λ�˿ͽ��н������涨��ÿλ�˿ʹ�һ��װ��4��������ֵ����Ĵ���һ�����������2���������������ֵ֮��Ϊ�ù˿�����Ľ����
��1����������װ��4��������1���������ֵΪ50Ԫ������3����Ϊ10Ԫ����
�ٹ˿�����Ľ�����Ϊ60Ԫ�ĸ��ʣ�
�ڹ˿�����Ľ�����ķֲ��м���ѧ������
��2���̳��Խ����ܶ��Ԥ����60000Ԫ�����涨���е�4����ֻ���ɱ�����ֵ10Ԫ��50Ԫ����������ɣ��������ֵ20Ԫ��40Ԫ����������ɣ�Ϊ��ʹ�˿͵õ��Ľ����ܶ���ܷ����̳���Ԥ����ÿλ�˿�����Ľ�������Ծ��⣬��Դ��е�4�������ֵ����һ�����ʵ���ƣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������Ǽ�����![]() ������ͼ��ֱ��ͼ.
������ͼ��ֱ��ͼ.

��1�����ж��߶�![]() ���Ƿ����һ��
���Ƿ����һ��![]() ��ʹ��
��ʹ��![]() ƽ��
ƽ��![]() ����˵�����ɣ�
����˵�����ɣ�
��2��֤����![]() .
.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com