Question

（本题满分14分）如图，α⊥β，α∩β=l ， A∈α， B∈β，点A在直线l 上的射影为A₁， 点B在l的射影为B₁，已知AB=2，AA₁=1， BB₁=， 求:

 (Ⅰ) 直线AB分别与平面α，β所成角的大小;

(Ⅱ)二面角A₁－AB－B₁的余弦值．

 

 

Answer 1

【答案】

解法一: (Ⅰ)如图， 连接A₁B，AB₁， ∵α⊥β， α∩β=l ,AA₁⊥l， BB₁⊥l，

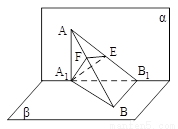∴AA₁⊥β， BB₁⊥α． 则∠BAB₁，∠ABA₁分别是AB与α和β所成的角．

Rt△BB₁A中， BB₁= ， AB=2， ∴sin∠BAB₁ = = ． ∴∠BAB₁=45°．

Rt△AA₁B中， AA₁=1，AB=2， sin∠ABA₁= = ， ∴∠ABA₁= 30°．

故AB与平面α，β所成的角分别是45°，30°．            ……………………………… 6分

(Ⅱ) ∵BB₁⊥α， ∴平面ABB₁⊥α．在平面α内过A₁作A₁E⊥AB₁交AB₁于E，则A₁E⊥平面AB₁B．过E作EF⊥AB交AB于F，连接A1F，则由三垂线定理得A₁F⊥AB， ∴∠A₁FE就是所求二面角的平面角．

在Rt△ABB₁中，∠BAB₁=45°，∴AB₁=B₁B=． ∴Rt△AA₁B中，A₁B== = ． 由AA₁·A₁B=A₁F·AB得 A₁F== = ，

∴在Rt△A1EF中，sin∠A₁FE = = ， ∴二面角A₁－AB－B₁的余弦值．

解法二: (Ⅰ)同解法一．

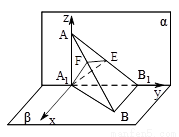
(Ⅱ) 如图，建立坐标系， 则A₁(0，0，0)，A(0，0，1)，B₁(0，1，0)，B(，1，0)．在AB上取一点F(x，y，z)，则存在t∈R，使得=t ， 即(x，y，z－1)=t(，1，－1)， ∴点F的坐标为(t， t，1－t)．要使⊥，须·=0， 即(t， t，1－t) ·(，1，－1)=0， 2t+t－(1－t)=0，解得t= ， ∴点F的坐标为(，－， )， ∴=(，， )． 设E为AB₁的中点，则点E的坐标为(0，， )． ∴=(，－，)．

又·=(，－，)·(，1，－1)= － － =0， ∴⊥， ∴∠A₁FE为所求二面角的平面角．

又cos∠A₁FE= = = = = ，

∴二面角A₁－AB－B₁的余弦值．                     ……………………………… 14

【解析】略