Question

2．已知正方体ABCD-A₁B₁C₁D₁，过A₁点可作    条直线与直线AC和BC₁都成60°角（　　）

• A． 1
• B． 2
• C． 3
• D． 4

Answer 1

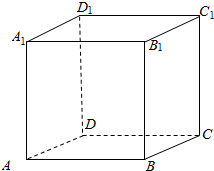
分析 因为AD₁∥BC₁，过A₁在空间作直线l，使l与直线AC和BC₁所成的角都等于 60⁰，可转化为过点A在空间作直线l，使l与直线AC和AD₁所成的角都等于 60⁰．可分在平面ACD₁内和在平面ACD₁外两种情况寻找．因为要与直线AC和AD₁所成的角都相等，故在平面ACD₁内可考虑角平分线；在平面AC1₁外可将角平分线绕点A旋转考虑．

解答 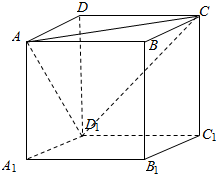解：因为AD₁∥BC₁，所以过A₁在空间作直线l，使l与直线AC和BC₁所
成的角都等于 60°，即过点A在空间作直线l，使l与直线AC和AD₁所
成的角都等于 60°．
因为∠CAD₁=60°，∠CAD₁的外角平分线与AC和AD₁所成的角相等，
均为60°，所以在平面ACD₁内有一条满足要求．
因为∠CAD₁的角平分线与AC和AD₁所成的角相等，均为30°，
将角平分线绕点A向上转动到与面ACD₁垂直的过程中，
存在两条直线与直线AC和AD₁所成的角都等于 60°；
故符合条件的直线有3条．
故选：C．

点评 本题考查异面直线所成角的问题，考查空间想象能力和转化能力．在解决本题的过程中，转化思想很重要，属于中档题．