
【题目】如图,三棱柱![]() 的所有棱长都是2,
的所有棱长都是2,![]() 面
面![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点.
的中点.
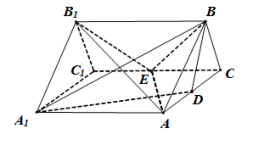
(1)求证:![]() 平面
平面![]() ;
;
(2)求三棱锥![]() 的体积.
的体积.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)推导出![]() ,从而平面
,从而平面![]() 平面
平面![]() ,进而
,进而![]() 平面
平面![]() ,
,![]() ,再求出
,再求出![]() ,由此能证明
,由此能证明![]() 平面
平面![]() .
.
(2)本问方法较多,可用割补法,转换顶点法,构造法等,其中割补法较为方便,将![]() 转化为
转化为![]() ,即可求解.
,即可求解.
解:(1)∵![]() ,
,![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,
∵三棱柱![]() 中
中![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴![]() .
.
又∵在正方形![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,
∴![]() ,
,
又![]() ,
,
∴![]() 平面
平面![]() .
.
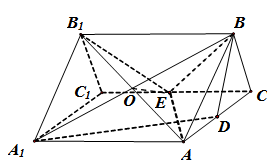
(2)解法一(割补法):
![]()
![]()
![]() .
.
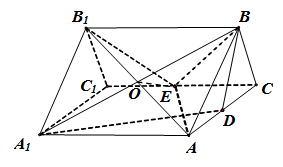
解法二(利用平行顶点轮换):
∵![]() ,
,
∴![]() ,
,
∴![]()
![]()
![]() .
.
解法三(利用对称顶点轮换):
连结![]() ,交
,交![]() 于点
于点![]() ,
,
∵![]() 为
为![]() 的中点,
的中点,
∴点![]() 到平面
到平面![]() 的距离等于点
的距离等于点![]() 到平面
到平面![]() 的距离.
的距离.
∴![]()
![]() .
.
解法四(构造法):
连结![]() ,交
,交![]() 于点
于点![]() ,则
,则![]() 为
为![]() 的中点,再连结
的中点,再连结![]() .
.
由题意知在![]() 中,
中,![]() ,
,![]() ,所以
,所以![]() ,且
,且![]() ,
,
又![]() ,
,![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
又![]() ,
,
∴![]() 面
面![]() ,
,
∴![]()
![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】等腰直角三角形BCD与等边三角形ABD中,![]() ,
,![]() ,现将
,现将![]() 沿BD折起,则当直线AD与平面BCD所成角为
沿BD折起,则当直线AD与平面BCD所成角为![]() 时,直线AC与平面ABD所成角的正弦值为( )
时,直线AC与平面ABD所成角的正弦值为( )
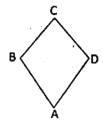
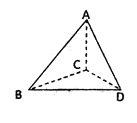
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】江南某湿地公园内有一个以![]() 为圆心,半径为20米的圆形湖心洲.该湖心洲的所对两岸近似两条平行线
为圆心,半径为20米的圆形湖心洲.该湖心洲的所对两岸近似两条平行线![]() ,且两平行线之间的距离为70米.公园管理方拟修建一条木栈道,其路线为
,且两平行线之间的距离为70米.公园管理方拟修建一条木栈道,其路线为![]() (如图,
(如图,![]() 在
在![]() 右侧).其中,
右侧).其中,![]() 与圆
与圆![]() 相切于点
相切于点![]() ,
,![]() 米.设
米.设![]() ,
,![]() 满足
满足![]() .
.
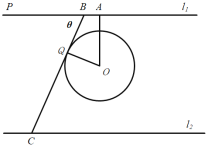
(1)试将木栈道![]() 的总长表示成关于
的总长表示成关于![]() 的函数
的函数![]() ,并指出其定义域;
,并指出其定义域;
(2)求木栈道![]() 总长的最短长度.
总长的最短长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在古代三国时期吴国的数学家赵爽创制了一幅“赵爽弦图”,由四个全等的直角三角形围成一个大正方形,中间空出一个小正方形(如图阴影部分)。若直角三角形中较小的锐角为a。现向大正方形区城内随机投掷一枚飞镖,要使飞镖落在小正方形内的概率为![]() ,则
,则![]() _____________。
_____________。
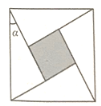
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过原点![]() 的动直线
的动直线![]() 与圆
与圆![]() :
: ![]() 交于
交于![]() 两点.
两点.
(1)若![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得当
,使得当![]() 变动时,总有直线
变动时,总有直线![]() 的斜率之和为0?若存在,求出
的斜率之和为0?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商店销售某海鲜,统计了春节前后50天该海鲜的需求量![]() (
(![]() ,单位:公斤),其频率分布直方图如图所示,该海鲜每天进货1次,商店每销售1公斤可获利50元;若供大于求,剩余的削价处理,每处理1公斤亏损10元;若供不应求,可从其它商店调拨,销售1公斤可获利30元.假设商店每天该海鲜的进货量为14公斤,商店的日利润为
,单位:公斤),其频率分布直方图如图所示,该海鲜每天进货1次,商店每销售1公斤可获利50元;若供大于求,剩余的削价处理,每处理1公斤亏损10元;若供不应求,可从其它商店调拨,销售1公斤可获利30元.假设商店每天该海鲜的进货量为14公斤,商店的日利润为![]() 元.
元.

(1)求商店日利润![]() 关于需求量
关于需求量![]() 的函数表达式;
的函数表达式;
(2)假设同组中的每个数据用该组区间的中点值代替.
①求这50天商店销售该海鲜日利润的平均数;
②估计日利润在区间![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四棱锥![]() 中,侧面
中,侧面![]() 底面
底面![]() ,底面
,底面![]() 是平行四边形,
是平行四边形,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 中点,点
中点,点![]() 在线段
在线段![]() 上.
上.
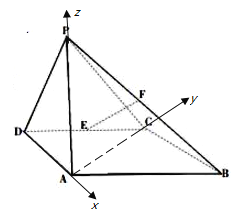
(Ⅰ)证明:![]() ;
;
(Ⅱ)若![]()
![]()
![]()
![]() ,求实数
,求实数![]() 使直线
使直线![]() 与平面
与平面![]() 所成角和直线
所成角和直线![]() 与平面
与平面![]() 所成角相等.
所成角相等.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com