
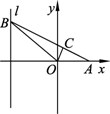
(经典回放)如图所示,给出定点A(a,0)(a>0)和直线l:x=-1,B是直线l上的动点,∠BOA的角平分线交AB于点C.求点C的轨迹方程,并讨论方程表示的曲线类型与a值的关系.
|
解析:依题意,记B(-1,b)(b∈R),则直线OA和OB的方程分别为y=0和y=-bx.设点C(x,y),则有0≤x<a,由OC平分∠AOB,知点C到OA、OB距离相等.根据点到直线的距离公式得 |y|= 依题设,点C在直线AB上,故有y= b= 将②式代入①式得y2[ 整理得y2[(1-a)x2-2ax+(1+a)y2]=0. 若y≠0,则(1-a)x2-2ax+(1+a)y2=0(0<x<a); 若y=0,则b=0,∠AOB=π,点C的坐标为(0,0),满足上式. 综上,得点C的轨迹方程为(1-a)x2-2ax+(1+a)y2=0(0≤x<a). ∵a≠1, ∴ 由此知,当0<a<1时,方程③表示椭圆弧段; 当a>1时,方程③表示双曲线一支的弧段. |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:全优设计必修四数学苏教版 苏教版 题型:044
(经典回放)已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,x∈R)在一个周期内的图象如下图所示.求直线y=3与函数y=f(x)的所有交点坐标.

查看答案和解析>>
科目:高中数学 来源:全优设计选修数学-2-2苏教版 苏教版 题型:022
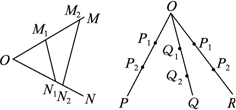
(经典回放)如图所示,若从点O所作的两条射线OM、ON上分别有点M1、M2与点N1、N2,则三角形面积之比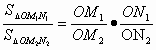 .若从点O所作的不在同一平面内的三条射线OP、OQ和OR上,分别有点P1、P2,点Q1、Q2和点R1、R2,则类似的结论为_________.
.若从点O所作的不在同一平面内的三条射线OP、OQ和OR上,分别有点P1、P2,点Q1、Q2和点R1、R2,则类似的结论为_________.
查看答案和解析>>
科目:高中数学 来源:全优设计选修数学-2-2苏教版 苏教版 题型:013
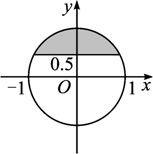
(经典回放)如图所示,与复平面中的阴影部分(含边界)对应的复数集合是_______(注:Rez表示z的实部,Imz表示z的虚部)
A.{z|z|=1,Rez≥![]() ,z∈C}
,z∈C}
B.{z|z|≤1,Rez≥![]() ,z∈C}
,z∈C}
C.{z|z|=1,Imz≥![]() ,z∈C}
,z∈C}
D.{z|z|≤1,Imz≥![]() ,z∈C}
,z∈C}
查看答案和解析>>
科目:高中数学 来源:全优设计选修数学-2-1苏教版 苏教版 题型:044
(经典回放)如图所示,在△ABC中,已知|AB|=![]() ,且内角满足2sinA+sinC=2sinB.试说明△ABC的顶点C的轨迹.
,且内角满足2sinA+sinC=2sinB.试说明△ABC的顶点C的轨迹.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com