练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，甲从A到B，乙从C到D，两人每次都只能向上或者向右走一格，如果两个人的线路不相交，则称这两个人的路径为一对孤立路，那么不同的孤立路一共有________对. （用数字作答）

    【答案】1750

    【解析】

    先分析甲乙分别到B,D的走法，各有种不同的走法，由分步乘法计数原理知共有路径，

    分析相同的路径，甲从A走到D与乙从C走到B的路径都相交，共有对相交路径，故孤立路共有.

    甲从A到B，需要向右走4步，向上走4步，共需8步，所以从A到B共有种走法，

    乙从C到D，需要向右走4步，向上走4步，共需8步，所以从A到B共有种走法，

    根据分步乘法计数原理可知，共有不同路径对，

    甲从A到D，需要向右走6步，向上走4步，共需10步，所以从A到D共有种走法,

    乙从C到B，需要向右走2步，向上走4步，共需6步，所以从C到B共有种走法,

    所以相交路径共有对，

    因此不同的孤立路一共有对.

    故答案为：1750

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某景区的各景点从2009年取消门票实行免费开放后，旅游的人数不断地增加，不仅带动了该市淡季的旅游，而且优化了旅游产业的结构，促进了该市旅游向“观光、休闲、会展”三轮驱动的理想结构快速转变．下表是从2009年至2018年，该景点的旅游人数（万人）与年份的数据：

    第年

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    旅游人数（万人）

    300

    283

    321

    345

    372

    435

    486

    527

    622

    800

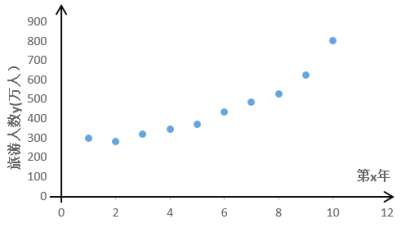
    该景点为了预测2021年的旅游人数，建立了与的两个回归模型：

    模型①：由最小二乘法公式求得与的线性回归方程；

    模型②：由散点图的样本点分布，可以认为样本点集中在曲线的附近．

    （1）根据表中数据，求模型②的回归方程．（精确到个位，精确到0．01）．

    （2）根据下列表中的数据，比较两种模型的相关指数，并选择拟合精度更高、更可靠的模型，预测2021年该景区的旅游人数（单位：万人，精确到个位）．

    回归方程

    ①

    ②

    30407

    14607

    参考公式、参考数据及说明：

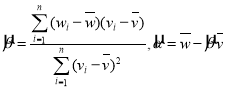    ①对于一组数据，其回归直线的斜率和截距的最小二乘法估计分别为．②刻画回归效果的相关指数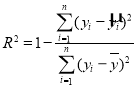；③参考数据：，．

    5．5

    449

    6．05

    83

    4195

    9．00

    表中．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为践行“绿水青山就是金山银山”的发展理念和提高生态环境的保护意识，高二年级准备成立一个环境保护兴趣小组.该年级理科班有男生400人，女生200人；文科班有男生100人，女生300人.现按男、女用分层抽样从理科生中抽取6人，按男、女分层抽样从文科生中抽取4人，组成环境保护兴趣小组，再从这10人的兴趣小组中抽出4人参加学校的环保知识竞赛.

    （1）设事件为“选出的这4个人中要求有两个男生两个女生，而且这两个男生必须文、理科生都有”，求事件发生的概率；

    （2）用表示抽取的4人中文科女生的人数，求的分布列和数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】以直角坐标系的原点为极点，x轴的非负半轴为极轴，建立极坐标系，并在两种坐标系中取相同的长度单位，已知直线l的参数方程为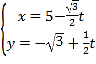（t为参数），圆C的极坐标方程为

    （1）求直线l和圆C的直角坐标方程；

    （2）若点在圆C上，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图6,四棱柱的所有棱长都相等,,四边形和四边形为矩形.

    (1)证明:底面;

    (2)若,求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】由于浓酸泄漏对河流形成了污染，现决定向河中投入固体碱，1个单位的固体碱在水中逐步溶化，水中的碱浓度与时间的关系，可近似地表示为，只有当河流中碱的浓度不低于1时，才能对污染产生有效的抑制作用.

    （1）如果只投放1个单位的固体碱，则能够维持有效抑制作用的时间有多长？

    （2）当河中的碱浓度开始下降时，即刻第二次投放1个单位的固体碱，此后，每一时刻河中的碱浓度认为是各次投放的碱在该时刻相应的碱浓度的和，求河中碱浓度可能取得的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】从金山区走出去的陈驰博士，在《自然—可持续性》杂志上发表的论文中指出：地球正在变绿，中国通过植树造林和提高农业效率，在其中起到了主导地位．已知某种树木的高度(单位：米)与生长年限（单位：年，tN*）满足如下的逻辑斯蒂函数：，其中e为自然对数的底数. 设该树栽下的时刻为0.

    （1）需要经过多少年，该树的高度才能超过5米？（精确到个位）

    （2）在第几年内，该树长高最快？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数，其中．

    （1）讨论函数的单调性；

    （2）当时，试证明：函数有且仅有两个零点，且．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数满足，.

    （1）若，，求实数的取值范围；

    （2）若有三个零点，求实数的取值范围.

    查看答案和解析>>

    同步练习册答案