
| A. | $\frac{1}{4}+\frac{1}{2}i$ | B. | $\frac{1}{2}+i$ | C. | $\frac{1}{4}-\frac{1}{2}i$ | D. | $\frac{1}{2}-i$ |
分析 设z=a+bi,(a,b∈R),则$\overline{z}=a-bi$,求出$3z+\overline{z}$,利用复数代数形式的乘除运算化简$\frac{4}{1-i}$,再由复数相等的充要条件即可求出a,b的值,则答案可求.
解答 解:设z=a+bi,(a,b∈R),则$\overline{z}=a-bi$,
∴$3z+\overline{z}=3a+3bi+a-bi=4a+2bi$,
$\frac{4}{1-i}$=$\frac{4(1+i)}{(1-i)(1+i)}=2+2i$,
∴4a+2bi=2+2i,
解得:a=$\frac{1}{2}$,b=1.
∴$z=\frac{1}{2}+i$.
故选:B.
点评 本题考查了复数代数形式的乘除运算,考查了复数相等的充要条件,是基础题.


科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD的底面ABCD是正方形,PA⊥底面ABCD,PA=AD,E、F分别是棱PD、BC的中点.
如图,四棱锥P-ABCD的底面ABCD是正方形,PA⊥底面ABCD,PA=AD,E、F分别是棱PD、BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$i | B. | 2$\sqrt{2}$ | C. | ±2$\sqrt{2}$i | D. | ±2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | -$\frac{2}{3}$ | D. | -$\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
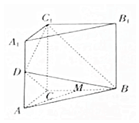 如图,在直三棱柱ABC-A1B1C1中,D,M分别是AA1,BC的中点,∠CDC1=90°,在△ABC中,AB=2AC,∠BAC=60°.
如图,在直三棱柱ABC-A1B1C1中,D,M分别是AA1,BC的中点,∠CDC1=90°,在△ABC中,AB=2AC,∠BAC=60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a<b,则a-1<b-1 | B. | 若a-1>b-1,则a>b | C. | 若a≤b,则a-1≤b-1 | D. | 若a-1≤b-1,则a≤b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com