
【题目】函数![]() 的导函数的图象如图所示,给出下列判断:
的导函数的图象如图所示,给出下列判断:
①函数![]() 在区间
在区间![]() 内单调递增;②函数
内单调递增;②函数![]() 在区间
在区间![]() 内单调递减;③函数
内单调递减;③函数![]() 在区间
在区间![]() 内单调递增;④当
内单调递增;④当![]() 时,函数
时,函数![]() 有极小值;⑤当
有极小值;⑤当![]() 时,函数
时,函数![]() 有极大值.则上述判断中正确的是( )
有极大值.则上述判断中正确的是( )
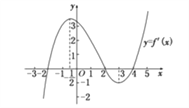
A. ①② B. ③
C. ②③ D. ③④⑤
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数),以
为参数),以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,且直线
,且直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(Ⅰ)求曲线![]() 的直角坐标方程及直线
的直角坐标方程及直线![]() 恒过的定点
恒过的定点![]() 的坐标;
的坐标;
(Ⅱ)在(Ⅰ)的条件下,若![]() ,求直线
,求直线![]() 的普通方程.
的普通方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市春节期间7家超市的广告费支出![]() (万元)和销售额
(万元)和销售额![]() (万元)数据如下:
(万元)数据如下:
超市 | A | B | C | D | E | F | G |
广告费支出 | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
销售额 | 19 | 32 | 40 | 44 | 52 | 53 | 54 |
(1)若用线性回归模型拟合![]() 与
与![]() 的关系,求
的关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)用二次函数回归模型拟合![]() 与
与![]() 的关系,可得回归方程:
的关系,可得回归方程:![]() ,
,
经计算二次函数回归模型和线性回归模型的![]() 分别约为
分别约为![]() 和
和![]() ,请用
,请用![]() 说明选择哪个回归模型更合适,并用此模型预测
说明选择哪个回归模型更合适,并用此模型预测![]() 超市广告费支出为3万元时的销售额.
超市广告费支出为3万元时的销售额.
参数数据及公式:![]() ,
,![]() ,
,
 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy上取两个定点![]() 再取两个动点
再取两个动点![]() ,
,![]() ,且
,且![]() .
.
(Ⅰ)求直线![]() 与
与![]() 交点M的轨迹C的方程;
交点M的轨迹C的方程;
(Ⅱ)过![]() 的直线与轨迹C交于P,Q,过P作
的直线与轨迹C交于P,Q,过P作![]() 轴且与轨迹C交于另一点N,F为轨迹C的右焦点,若
轴且与轨迹C交于另一点N,F为轨迹C的右焦点,若![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区以“绿色出行”为宗旨开展“共享单车”业务.该地区某高级中学一兴趣小组由9名高二级学生和6名高一级学生组成,现采用分层抽样的方法抽取5人,组成一个体验小组去市场体验“共享单车”的使用.问:
(Ⅰ)应从该兴趣小组中抽取高一级和高二级的学生各多少人;
(Ⅱ)已知该地区有![]() ,
, ![]() 两种型号的“共享单车”,在市场体验中,该体验小组的高二级学生都租
两种型号的“共享单车”,在市场体验中,该体验小组的高二级学生都租![]() 型车,高一级学生都租
型车,高一级学生都租![]() 型车.如果从组内随机抽取2人,求抽取的2人中至少有1人在市场体验过程中租
型车.如果从组内随机抽取2人,求抽取的2人中至少有1人在市场体验过程中租![]() 型车的概率.
型车的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,用K、A1、A2三类不同的元件连接成一个系统.当K正常工作且A1、A2至少有一个正常工作时,系统正常工作,已知K、A1、A2正常工作的概率依次是0.9、0.8、0.8,则系统正常工作的概率为( )
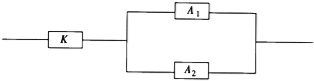
A. 0.960 B. 0.864 C. 0.720 D. 0.576
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com