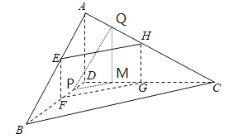
【题目】在四面体ABCD中，过棱AB的上一点E作平行于AD，BC的平面分别交四面体的棱BD，DC，CA于点F，G，H
（1）求证：截面EFGH为平行四边形
（2）若P、Q在线段BD、AC上，
，且P、F不重合，证明：PQ∥截面EFGH
【答案】（1）见解析；（2）见解析
【解析】
（1）利用线面平行的性质定理得出线线平行，再利用平行公理得出又一组线线平行，有两组对边互相平行即可得证.
(2)先由题目中的比例证得两组线线平行，由面面平行的判定定理即可得证.
（1）证明：∵AD∥平面EFGH，平面ADB
平面EHGH=EF，AD
平面ABD，
∴AD∥EF ∵AD∥平面EHGH，平面ADC平面EHGH=GH，AD平面ADC，. ∴AD∥GH
由平行公理可得EF∥GH
同理可得EH∥FG
∴四边形EFGH为平行四边形.
（2）如图在CD上取点M，使
，连接MQ
则PM∥BC∥FG，
，则QM∥AD∥HG
PMQM=M∴平面PMQ∥平面EHGH
∵PQ平面PMQ
∴PQ∥截面EFGH
科目：高中数学 来源： 题型：
【题目】某市为增强市民的环境保护意识，面向全市征召义务宣传志愿者．现从符合条件的志愿者中随机抽取100名按年龄分组：第
组
，第
组
，第
组
，第
组
，第
组
，得到的频率分布直方图如图所示．
(1)若从第3，4，5组中用分层抽样的方法抽取6名志愿者参加广场的宣传活动，应从第3，4，5组各抽取多少名志愿者？
(2)在（1）的条件下，该市决定在第3，4组的志愿者中随机抽取2名志愿者介绍宣传经验，求第4组至少有一名志愿者被抽中的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】己知在平面直角坐标系
中,圆
的参数方程为
(
为参数)以
轴为极轴， 
为极点建立极坐标系,在该极坐标系下,圆
是以点
为圆心,且过点
的圆心.
(1)求圆
及圆
在平而直角坐标系
下的直角坐标方程；
(2)求圆
上任一点
与圆
上任一点之间距离的最小值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，直线l的参数方程为
（t为参数），以坐标原点为极点，x轴正半轴为极轴建立极坐标系，圆
的极坐标方程为
．
（1）若直线l与圆相切，求
的值；
（2）若直线l与曲线
（为参数）交于A，B两点，点
，求
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，AB为⊙O的直径，过点B作⊙O的切线BC，OC交⊙O于点E，AE的延长线交BC于点D． 
（1）求证：CE2=CDCB．
（2）若AB=2，BC= 
，求CE与CD的长．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】甲、乙两运动员进行射击训练．已知他们击中的环数都稳定在
，
，
环，且每次射击击中与否互不影响．甲、乙射击命中环数的概率如下表：
（
）若甲、乙两运动员各射击次，求甲运动员击中环且乙运动员击中环的概率．
（
）若甲射击
次，用
表示这次射击击中环以上（含环）的次数，求随机变量的分布列及期望．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】直三棱柱ABC﹣A1B1C1中，∠BCA=90°，M、N分别是A1B1、A1C1的中点，BC=AC=CC1 ， 则CN与AM所成角的余弦值等于（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，四棱锥P﹣ABCD的底面ABCD为矩形，PA⊥平面ABCD，点E是棱PD的中点，点F是PC的中点F． 
（1）证明：PB∥平面AEC；
（2）若ABCD为正方形，探究在什么条件下，二面角C﹣AF﹣D大小为60°？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
