
| A�� | ��P��0��0��Ϊ����C��y=x3�ġ����ƹյ㡱 | |
| B�� | ��P��0��0��Ϊ����C��y=sinx�ġ����ƹյ㡱 | |
| C�� | ��P��0��0��Ϊ����C��y=tanx�ġ����ƹյ㡱 | |
| D�� | ��P��1��0��Ϊ����C��y=lnx�ġ����ƹյ㡱 |
���� �ֱ����ÿһ������������C�ĵ������õ������ڵ�P���ĵ���ֵ����������ڵ�P�������߷��̣����������ڵ�P����ĺ���ֵ���Ӧֱ���ϵ��ֵ�Ĵ�С�ж��Ƿ����㣨ii�������жϳ�ѡ���Ƿ�������⣮
��� �⣺A����y=x3��y��=3x2����y��|x=0=0��ֱ��y=0�ǹ���P��0��0��������C�����ߣ�
�ֵ�x��0ʱy��0����x��0ʱy��0����������C��P��0��0������λ��ֱ��y=0���࣬A���������⣻
B����y=sinx��y��=cosx����y��|x=��=-1��ֱ��y=-x+���ǹ���P��0��0�������ߵ����ߣ�
��x�ʣ�-$\frac{��}{2}$��0��ʱx��sinx��x�ʣ�0��$\frac{��}{2}$��ʱx��sinx��
��������C��P��0��0������λ��ֱ��y=-x+�����࣬B���������⣻
C����y=tanx��y��=sec2x����y��|x=0=1��ֱ��y=x�ǹ���P��0��0�������ߵ����ߣ�
��x�ʣ�-$\frac{��}{2}$��0��ʱx��tanx��x�ʣ�0��$\frac{��}{2}$��ʱx��tanx��
��������C��P��0��0������λ��ֱ��y=x���࣬C���������⣻
D����y=lnx��y��=$\frac{1}{x}$����y��|x=1=1��������P��1��0����������Ϊy=x-1��
��g��x��=x-1-lnx����g�䣨x��=1-$\frac{1}{x}$��
��x�ʣ�0��1��ʱ��g�䣨x����0����x�ʣ�1��+�ޣ�ʱ��g�䣨x����0��
��g��x���ڣ�0��+�ޣ����м�СֵҲ����Сֵ��Ϊg��1��=0��
��y=x-1����y=lnx���Ϸ�������������C�ڵ�P����λ��ֱ��l�����࣬D�������⣬
��ѡ��D��
���� ���⿼�������õ����о���������ij�㴦�����߷��̣��ۺϿ��鵼����Ӧ�ã�������ͼ�ֵ����ֵ��ͬʱ�����¶�������⣬�����е�����״��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ������S-ABCD�У�����ABCD�����Σ���Խ��ߵĽ���ΪO����SA=SC��SA��BD��
��ͼ������S-ABCD�У�����ABCD�����Σ���Խ��ߵĽ���ΪO����SA=SC��SA��BD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
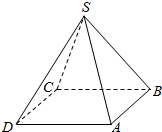 ��ͼ��ʾ�����һ����������ˮ�������������ĵ����������Σ�������ȫ�ȵĵ��������Σ���֪����߳�Ϊ2m����Ϊ$\sqrt{7}$m����֤��
��ͼ��ʾ�����һ����������ˮ�������������ĵ����������Σ�������ȫ�ȵĵ��������Σ���֪����߳�Ϊ2m����Ϊ$\sqrt{7}$m����֤���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com