
 在△PMN中,|MN|=6,
在△PMN中,|MN|=6,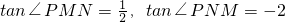 .建立适当坐标系,
.建立适当坐标系, 解:(1)如图,以直线MN为x轴,MN的垂直平分线为y轴,建立直角坐标系.
解:(1)如图,以直线MN为x轴,MN的垂直平分线为y轴,建立直角坐标系. +
+ =1,焦点为M(-3,0),N(3,0)
=1,焦点为M(-3,0),N(3,0) ,tanα=tan(π-∠MNP)=2,
,tanα=tan(π-∠MNP)=2, (x+3)①,
(x+3)①, ,|PN|=2
,|PN|=2 ,
,
 +
+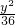 =1.
=1. +
+ =1,点P(5,4)代入得a=3
=1,点P(5,4)代入得a=3 ,
, +
+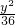 =1.
=1. ,tan∠PNM=-2即可求得直线MP和直线NP的方程;
,tan∠PNM=-2即可求得直线MP和直线NP的方程; +
+ =1,点P(5,4)代入即可求之.
=1,点P(5,4)代入即可求之.

 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:高中数学 来源: 题型:
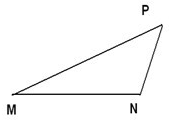 在△PMN中,|MN|=6,tan∠PMN=
在△PMN中,|MN|=6,tan∠PMN=| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省济宁市汶上一中高二(上)期中数学试卷(理科)(解析版) 题型:解答题
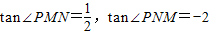 .建立适当坐标系,
.建立适当坐标系,
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com