
|
| 1 |
| x |
| 1 |
| e |
| 1 |
| e |
| 1 |
| e |
| 1 |
| e |
| 1 |
| e |
| 1 |
| e |
| 1 |
| e |
| 1 |
| e |
| 1 |
| e |
| 1 |
| e |
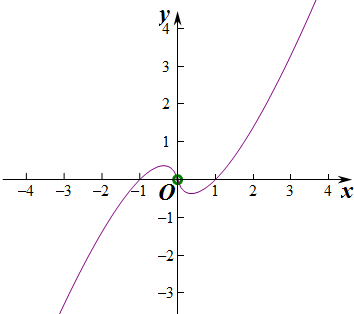 ∵当x>0时,当x=
∵当x>0时,当x=| 1 |
| e |
| 1 |
| e |
| 1 |
| e |
| 1 |
| e |
| 1 |
| e |


科目:高中数学 来源: 题型:
| π |
| 12 |
| π |
| 4 |
| MP |
| MQ |
| PQ |
A、f(
| ||||
B、f(
| ||||
C、f(
| ||||
D、f(-
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、0 | ||
| B、1 | ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| 2 |
| 1 |
| 2 |
| π |
| 6 |
| ||
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
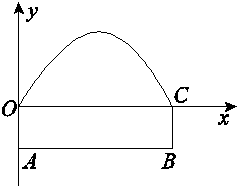 有一条双向公路隧道,其横断面由抛物线和矩形ABCO的三边组成,隧道的最大高度为4.9m,AB=10m,BC=2.4m.现把隧道的横断面放在平面直角坐标系中,若有一辆高为4m,宽为2m的装有集装箱的汽车要通过隧道.问:如果不考虑其他因素,汽车的右侧离开隧道右壁至少多少米才不至于碰到隧道顶部(抛物线部分为隧道顶部,AO、BC为壁)?
有一条双向公路隧道,其横断面由抛物线和矩形ABCO的三边组成,隧道的最大高度为4.9m,AB=10m,BC=2.4m.现把隧道的横断面放在平面直角坐标系中,若有一辆高为4m,宽为2m的装有集装箱的汽车要通过隧道.问:如果不考虑其他因素,汽车的右侧离开隧道右壁至少多少米才不至于碰到隧道顶部(抛物线部分为隧道顶部,AO、BC为壁)?查看答案和解析>>
科目:高中数学 来源: 题型:
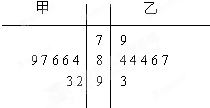 如图是校园“十佳歌手”大奖赛上,七位评委为甲、乙两位选手打出的分数的茎叶图.
如图是校园“十佳歌手”大奖赛上,七位评委为甲、乙两位选手打出的分数的茎叶图.查看答案和解析>>
科目:高中数学 来源: 题型:
| an+2-an+1 |
| an+1-an |
| A、0 | B、1 | C、2 | D、3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com