
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且asinAcosC+csinAcosA= ![]() c,D是AC的中点,且cosB=
c,D是AC的中点,且cosB= ![]() ,BD=
,BD= ![]() .
.
(1)求角A的大小;
(2)求△ABC的最短边的边长.
【答案】
(1)解:∵cosB= ![]() ,
,
∴sinB= ![]() ,
,
又∵asinAcosC+csinAcosA= ![]() c,
c,
∴正弦定理化简可得:sinAcosCsinA+sinAsinCcosA= ![]() sinC.
sinC.
即sinA(cosCsinA+sinCcosA)= ![]() sinC
sinC
∴sinAsinB= ![]() sinC,
sinC,
∵A+B+C=π,
∴C=π﹣(A+B)
∴sinAsinB= ![]() sin(A+B)
sin(A+B)
![]() sinA=
sinA= ![]() sinAcosB+
sinAcosB+ ![]() cosAsinB,
cosAsinB,
∴sinA=cosA.
即tanA=1,
∵0<A<π,
∴A= ![]() .
.
(2)D是AC的中点,且cosB= ![]() ,BD=
,BD= ![]() ,
,
根据余弦定理得c2+ ![]() b2﹣
b2﹣ ![]() bc=26
bc=26
∵ ![]() sinA=
sinA= ![]() sinC,且sinB×
sinC,且sinB× ![]() =
= ![]() sinC
sinC
∴ ![]()
解得:a=2 ![]() .
.
b=2 ![]() ,
,
c=6
∴△ABC的最短边的边长2 ![]() .
.
【解析】(1)利用正弦定理化简并根据和与差的公式即可求出角A的值。(2)根据余弦定理建立关系求解出a、b、c的值即可得到△ABC的最短边的边长。


科目:高中数学 来源: 题型:
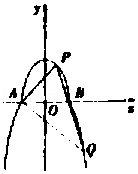
【题目】如图,曲线C由上半椭圆 ![]() 和部分抛物线
和部分抛物线 ![]() 连接而成,C1与C2的公共点为A,B,其中C1的离心率为
连接而成,C1与C2的公共点为A,B,其中C1的离心率为 ![]() .
.
(1)求a,b的值;
(2)过点B的直线l与C1 , C2分别交于点P,Q(均异于点A,B),是否存在直线l,使得PQ为直径的圆恰好过点A,若存在直线l的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,摄影爱好者S在某公园A处,发现正前方B处有一立柱,测得立柱顶端O的仰角和立柱底部B的俯角均为 ![]() .设S的眼睛到地面的距离为
.设S的眼睛到地面的距离为 ![]() 米
米
(1)求摄影爱好者到立柱的水平距离和立柱的高度;
(2)立柱的顶端有一长2米的彩杆MN绕其中点O在S与立柱所在的平面内旋转.摄影爱好者有一视角范围为 ![]() 的镜头,在彩杆转动的任意时刻,摄影爱好者是否都可以将彩杆全部摄入画面?请说明理由.
的镜头,在彩杆转动的任意时刻,摄影爱好者是否都可以将彩杆全部摄入画面?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设圆x2+y2=12与抛物线x2=4y相交于A,B两点,F为抛物线的焦点,若过点F且斜率为1的直线l与抛物线和圆交于四个不同的点,从左至右依次为P1 , P2 , P3 , P4 , 则|P1P2|+|P3P4|的值 , 若直线m与抛物线相交于M,N两点,且与圆相切,切点D在劣弧 ![]() 上,则|MF|+|NF|的取值范围是 .
上,则|MF|+|NF|的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=ln(x+m)﹣nlnx.
(1)当m=1,n>0时,求函数f(x)的单调减区间;
(2)n=1时,函数g(x)=(m+2x)f(x)﹣am,若存在m>0,使得g(x)>0恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班为了提高学生学习英语的兴趣,在班内举行英语写、说、唱综合能力比赛,比赛分为预赛和决赛2个阶段,预赛为笔试,决赛为说英语、唱英语歌曲,将所有参加笔试的同学进行统计,得到频率分布直方图,其中后三个矩形高度之比依次为4:2:1,落在[80,90)的人数为12人.
(Ⅰ)求此班级人数;
(Ⅱ)按规定预赛成绩不低于90分的选手参加决赛,已知甲乙两位选手已经取得决赛资格,参加决赛的选手按抽签方式决定出场顺序.
(i)甲不排在第一位乙不排在最后一位的概率;
(ii)记甲乙二人排在前三位的人数为X,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆的左焦点为F1 , 有一小球A从F1处以速度v开始沿直线运动,经椭圆壁反射(无论经过几次反射速度大小始终保持不变,小球半径忽略不计),若小球第一次回到F1时,它所用的最长时间是最短时间的5倍,则椭圆的离心率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从0,1,2,3,4这五个数中任选三个不同的数组成一个三位数,记Y为所组成的三位数各位数字之和.
(1)求Y是奇数的概率;
(2)求Y的概率分布和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com