
分析 (1)利用f(x+2)=-f(x),可由x∈[0,2]时的解析式求x∈[-2,0]时的解析式;
(2)配方,即可画出函数的图象.
解答 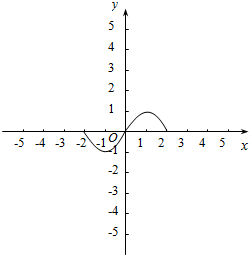 解:(1)因为x∈[0,2]时,f(x)=2x-x2,
解:(1)因为x∈[0,2]时,f(x)=2x-x2,
所以x∈[-2,0]时,x+2∈[0,2],
则f(x+2)=2(x+2)-(x+2)2
=-x2-2x,x∈[-2,0]
又f(x+2)=-f(x),
所以f(x)=x2+2x,x∈[-2,0].
(2)x∈[0,2]时,f(x)=2x-x2=-(x-1)2+1
求x∈[-2,0)时,f(x)=x2+2x=(x+1)2-1.
如图所示
点评 本题综合考查函数奇偶性与周期性知识的运用,考查学生的作图能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
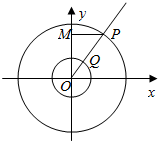 如图所示,以原点O为圆心的两个同心圆的半径分别为3和1,过原点O的射线交大圆于点P,交小圆于点Q,P在y轴上的射影为M,动点N满足$\overrightarrow{PM}$=λ$\overrightarrow{PN}$且$\overrightarrow{PM}$•$\overrightarrow{QN}$=0.
如图所示,以原点O为圆心的两个同心圆的半径分别为3和1,过原点O的射线交大圆于点P,交小圆于点Q,P在y轴上的射影为M,动点N满足$\overrightarrow{PM}$=λ$\overrightarrow{PN}$且$\overrightarrow{PM}$•$\overrightarrow{QN}$=0.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 574 | B. | 576 | C. | 1088 | D. | 1090 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com