
【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c,cosB=![]() .
.
(Ⅰ)若c=2a,求![]() 的值;
的值;
(Ⅱ)若C-B=![]() ,求sinA的值.
,求sinA的值.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)由余弦定理结合![]() ;可得
;可得![]() ,再由正弦定理可得结果;(2)先由
,再由正弦定理可得结果;(2)先由![]() ,根据二倍角公式可得
,根据二倍角公式可得![]() ,则
,则![]() ,根据两角差的正弦公式可得结果.
,根据两角差的正弦公式可得结果.
试题解析:(1)解法1
在△ABC中,因为cosB=![]() ,所以
,所以![]() =
=![]() .
.
因为c=2a,所以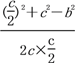 =
=![]() ,即
,即![]() =
=![]() ,
,
所以![]() =
=![]() .
.
又由正弦定理得![]() =
=![]() ,
,
所以![]() =
=![]() .
.
解法2
因为cosB=![]() ,B∈(0,),所以sinB=
,B∈(0,),所以sinB=![]() =
=![]() .
.
因为c=2a,由正弦定理得sinC=2sinA,
所以sinC=2sin(B+C)=![]() cosC+
cosC+![]() sinC,
sinC,
即-sinC=2cosC.
又因为sin2C+cos2C=1,sinC>0,解得sinC=![]() ,
,
所以![]() =
=![]() .
.
(2)因为cosB=![]() ,所以cos2B=2cos2B-1=
,所以cos2B=2cos2B-1=![]() .
.
又0<B<π,所以sinB=![]() =
=![]() ,
,
所以sin2B=2sinBcosB=2×![]() ×
×![]() =
=![]() .
.
因为C-B=![]() ,即C=B+
,即C=B+![]() ,所以A=π-(B+C)=
,所以A=π-(B+C)=![]() -2B,
-2B,
所以sinA=sin(![]() -2B)
-2B)
=sin![]() cos2B-cos
cos2B-cos![]() sin2B
sin2B
=![]() ×
×![]() -(-
-(-![]() )×
)×![]()
=![]() .
.


科目:高中数学 来源: 题型:
【题目】已知曲线C 的参数方程为 (
(![]() 为参数),以直角坐标系原点O 为极点,x 轴正半轴为极轴建立极坐标系.
为参数),以直角坐标系原点O 为极点,x 轴正半轴为极轴建立极坐标系.
(Ⅰ)求曲线C 的极坐标方程;
(Ⅱ)设![]() ,若l 1 、l2与曲线C 相交于异于原点的两点 A、B ,求△AOB的面积.
,若l 1 、l2与曲线C 相交于异于原点的两点 A、B ,求△AOB的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数f(x)= ![]() (a∈R)是奇函数,函数g(x)=
(a∈R)是奇函数,函数g(x)= ![]() 的定义域为(﹣2,+∞).
的定义域为(﹣2,+∞).
(1)求a的值;
(2)若g(x)= ![]() 在(﹣2,+∞)上单调递减,根据单调性的定义求实数m的取值范围;
在(﹣2,+∞)上单调递减,根据单调性的定义求实数m的取值范围;
(3)在(2)的条件下,若函数h(x)=f(x)+g(x)在区间(﹣1,1)上有且仅有两个不同的零点,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某产品关税与市场供应量P的关系近似地满足:P(x)=2 ![]() (其中t为关税的税率,且t∈[0,
(其中t为关税的税率,且t∈[0, ![]() ],x为市场价格,b,k为正常数),当t=
],x为市场价格,b,k为正常数),当t= ![]() 时,市场供应量曲线如图所示:
时,市场供应量曲线如图所示: 
(1)根据函数图象求k,b的值;
(2)若市场需求量Q,它近似满足Q(x)=2 ![]() .当P=Q时的市场价格为均衡价格,为使均衡价格控制在不低于9元的范围内,求税率t的最小值.
.当P=Q时的市场价格为均衡价格,为使均衡价格控制在不低于9元的范围内,求税率t的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,椭圆C:![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,且过点(1,
,且过点(1,![]() ).过椭圆C的左顶点A作直线交椭圆C于另一点P,交直线l:x=m(m>a)于点M.已知点B(1,0),直线PB交l于点N.
).过椭圆C的左顶点A作直线交椭圆C于另一点P,交直线l:x=m(m>a)于点M.已知点B(1,0),直线PB交l于点N.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若MB是线段PN的垂直平分线,求实数m的值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点![]() 到定点
到定点![]() 的距离比
的距离比![]() 到定直线
到定直线![]() 的距离小1.
的距离小1.
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)过点![]() 任意作互相垂直的两条直线
任意作互相垂直的两条直线![]() ,分别交曲线
,分别交曲线![]() 于点
于点![]() 和
和![]() .设线段
.设线段![]() ,
, ![]() 的中点分别为
的中点分别为![]() ,求证:直线
,求证:直线![]() 恒过一个定点;
恒过一个定点;
(Ⅲ)在(Ⅱ)的条件下,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知下列四个命题:
p1:若直线l和平面α内的无数条直线垂直,则l⊥α;
p2:若f(x)=2x﹣2﹣x , 则x∈R,f(﹣x)=﹣f(x);
p3:若 ![]() ,则x0∈(0,+∞),f(x0)=1;
,则x0∈(0,+∞),f(x0)=1;
p4:在△ABC中,若A>B,则sinA>sinB.
其中真命题的个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com