
【题目】已知sin(x﹣ ![]() )=
)= ![]() ,cos2x=
,cos2x= ![]() , (Ⅰ)求
, (Ⅰ)求 ![]() 的值;
的值;
(Ⅱ)求 ![]() 的值.
的值.
【答案】解:(Ⅰ)∵sin(x﹣ ![]() )=
)= ![]() ,
, ![]() (sinx﹣cosx)=
(sinx﹣cosx)= ![]() ,
,
sinx﹣cosx= ![]() ①,
①,
1﹣2sinxcosx= ![]() ,
,
sinxcosx=﹣ ![]() ②,
②,
∴由①②可得:cox<0,
又∵cos2x=2cos2x﹣1= ![]() ,解得:cosx=﹣
,解得:cosx=﹣ ![]() ,由①可得:sinx=
,由①可得:sinx= ![]() ,
,
∴ ![]()
=cos( ![]() +
+ ![]() ﹣x)
﹣x)
=cos ![]() cos(
cos( ![]() ﹣x)﹣sin
﹣x)﹣sin ![]() sin(
sin( ![]() ﹣x)
﹣x)
= ![]() cos(x﹣
cos(x﹣ ![]() )+
)+ ![]() sin(x﹣
sin(x﹣ ![]() )
)
= ![]() ×
× ![]() (﹣
(﹣ ![]() +
+ ![]() )+
)+ ![]() ×
× ![]()
= ![]() .
.
(Ⅱ)∵由(Ⅰ)可得:cosx=﹣ ![]() ,sinx=
,sinx= ![]() ,
,
∴ ![]() =
= 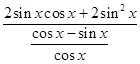 =﹣
=﹣ ![]()
【解析】(Ⅰ)由已知等式利用特殊角的三角函数值,两角差的正弦函数公式化简可得sinx﹣cosx= ![]() ,两边平方可得sinxcosx=﹣
,两边平方可得sinxcosx=﹣ ![]() ,结合cos2x=
,结合cos2x= ![]() ,利用二倍角的余弦函数公式可求cosx,sinx的值, 由特殊角的三角函数值,两角和与差的余弦函数公式即可化简求值.(Ⅱ)由(Ⅰ)cosx,sinx的值,利用同角三角函数基本关系式,倍角公式即可化简求值.
,利用二倍角的余弦函数公式可求cosx,sinx的值, 由特殊角的三角函数值,两角和与差的余弦函数公式即可化简求值.(Ⅱ)由(Ⅰ)cosx,sinx的值,利用同角三角函数基本关系式,倍角公式即可化简求值.


科目:高中数学 来源: 题型:
【题目】小丽今天晚自习准备复习历史、地理或政治中的一科,她用数学游戏的结果来决定选哪一科,游戏规则是:在平面直角坐标系中,以原点![]() 为起点,再分别以
为起点,再分别以![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 这5个点为终点,得到5个向量,任取其中两个向量,计算这两个向量的数量积
这5个点为终点,得到5个向量,任取其中两个向量,计算这两个向量的数量积![]() ,若
,若![]() ,就复习历史,若
,就复习历史,若![]() ,就复习地理,若
,就复习地理,若![]() ,就复习政治.
,就复习政治.
(1)写出![]() 的所有可能取值;
的所有可能取值;
(2)求小丽复习历史的概率和复习地理的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出以下说法:①不共面的四点中,任意三点不共线;
②有三个不同公共点的两个平面重合;
③没有公共点的两条直线是异面直线;
④分别和两条异面直线都相交的两条直线异面;
⑤一条直线和两条异面直线都相交,则它们可以确定两个平面.
其中正确结论的序号是_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【河南省豫南九校(中原名校)2017届高三下学期质量考评八数学(文)】已知双曲线![]() 的左右两个顶点是
的左右两个顶点是![]() ,
, ![]() ,曲线
,曲线![]() 上的动点
上的动点![]() 关于
关于![]() 轴对称,直线
轴对称,直线![]() 与
与![]() 交于点
交于点![]() ,
,
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)点![]() ,轨迹
,轨迹![]() 上的点
上的点![]() 满足
满足![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{xn}满足x1=1,x2=λ,并且 ![]() =λ
=λ ![]() (λ为非零常数,n=2,3,4,…). (Ⅰ)若x1 , x3 , x5成等比数列,求λ的值;
(λ为非零常数,n=2,3,4,…). (Ⅰ)若x1 , x3 , x5成等比数列,求λ的值;
(Ⅱ)设0<λ<1,常数k∈N* , 证明 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据下列条件求双曲线的标准方程:
(1)经过点(![]() ,3),且一条渐近线方程为4x+3y=0.
,3),且一条渐近线方程为4x+3y=0.
(2)P(0,6)与两个焦点的连线互相垂直,与两个顶点连线的夹角为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
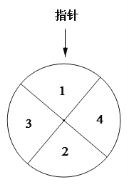
【题目】【2016高考山东文数】某儿童乐园在“六一”儿童节推出了一项趣味活动.参加活动的儿童需转动如图所示的转盘两次,每次转动后,待转盘停止转动时,记录指针所指区域中的数.设两次记录的数分别为x,y.奖励规则如下:
①若![]() ,则奖励玩具一个;
,则奖励玩具一个;
②若![]() ,则奖励水杯一个; ③其余情况奖励饮料一瓶.
,则奖励水杯一个; ③其余情况奖励饮料一瓶.
假设转盘质地均匀,四个区域划分均匀.小亮准备参加此项活动.
(I)求小亮获得玩具的概率;
(II)请比较小亮获得水杯与获得饮料的概率的大小,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com