
【题目】(1)求与椭圆![]() 有共同焦点且过点
有共同焦点且过点![]() 的双曲线的标准方程;
的双曲线的标准方程;
(2)已知抛物线的焦点在![]() 轴上,抛物线上的点
轴上,抛物线上的点![]() 到焦点的距离等于5,求抛物线的标准方程和
到焦点的距离等于5,求抛物线的标准方程和![]() 的值.
的值.
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C的参数方程为![]() ,(θ为参数),以原点为极点,x轴非负半轴为极轴建立极坐标系.
,(θ为参数),以原点为极点,x轴非负半轴为极轴建立极坐标系.
(1)求曲线C的极坐标方程;
(2)在平面直角坐标系xOy中,A(﹣2,0),B(0,﹣2),M是曲线C上任意一点,求△ABM面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】厂家在产品出厂前,需对产品做检验,厂家将一批产品发给商家时,商家按合同规定也需随机抽取一定数量的产品做检验,以决定是否接收这批产品.
(1)若厂家库房中(视为数量足够多)的每件产品合格的概率为 ![]() 从中任意取出 3件进行检验,求至少有
从中任意取出 3件进行检验,求至少有![]() 件是合格品的概率;
件是合格品的概率;
(2)若厂家发给商家![]() 件产品,其中有
件产品,其中有![]() 不合格,按合同规定 商家从这
不合格,按合同规定 商家从这![]() 件产品中任取
件产品中任取![]() 件,都进行检验,只有
件,都进行检验,只有![]() 件都合格时才接收这批产品,否则拒收.求该商家可能检验出的不合格产品的件数ξ的分布列,并求该商家拒收这批产品的概率.
件都合格时才接收这批产品,否则拒收.求该商家可能检验出的不合格产品的件数ξ的分布列,并求该商家拒收这批产品的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1.则该半正多面体共有________个面,其棱长为_________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了展示中华汉字的无穷魅力,传递传统文化,提高学习热情,某校开展“中国汉字听写大会”的活动,为响应学校号召,某班组建了兴趣班,根据甲、乙两人近期6次成绩画出的茎叶图如图所示,甲的成绩中有一个数的个位数字模糊,在茎叶图中用a表示.已知甲、乙两人成绩的平均数相同.
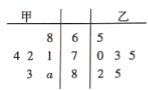
(1)根据题目信息,求a的值;
(2)现要从甲、乙两人中选派一人参加比赛,从稳定性的角度,你认为派谁参加比赛较合适?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国2019年新年贺岁大片《流浪地球》自上映以来引发了社会的广泛关注,受到了观众的普遍好评.假设男性观众认为《流浪地球》好看的概率为![]() ,女性观众认为《流浪地球》好看的概率为
,女性观众认为《流浪地球》好看的概率为![]() .某机构就《流浪地球》是否好看的问题随机采访了4名观众.
.某机构就《流浪地球》是否好看的问题随机采访了4名观众.
(1)若这4名观众2男2女,求这4名观众中女性认为好看的人数比男性认为好看的人数多的概率;
(2)若这4名观众都是男性,设X表示这4名观众中认为《流浪地球》好看的人数,求X的分布列与数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com