
【题目】
已知函数![]() ,
,![]() .
.
(1)若曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直,求
垂直,求![]() 的值;
的值;
(2)若![]() 存在极小值
存在极小值![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)当![]() 时,如果存在两个不相等的正数
时,如果存在两个不相等的正数![]() ,使得
,使得![]() ,求证:
,求证:![]() .
.
请考生在第22、23两题中任选一题作答.注意:只能做所选定的题目.如果多做,则按所做的第一个题目计分.
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C的方程为y2=10x,直线l的参数方程为 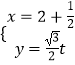 (t为参数),以坐标原点为极点,以x轴的正半轴为极轴建立极坐标系.
(t为参数),以坐标原点为极点,以x轴的正半轴为极轴建立极坐标系.
(1)求曲线C的极坐标方程和直线l的普通方程;
(2)设直线l与曲线C交于A、B两点,求弦长|AB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+bx+1(a,b∈R且a≠0),F(x)= ![]() .
.
(1)若f(﹣1)=0,且函数f(x)的值域为[0,+∞),求F(x)的解析式;
(2)在(1)的条件下,当x∈[﹣2,2]时,g(x)=f(x)﹣kx是单调函数,求实数k的取值范围;
(3)设mn<0,m+n>0,a>0,且f(x)是偶函数,判断F(m)+F(n)是否大于零.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“累计净化量(CCM)”是空气净化器质量的一个重要衡量指标,它是指空气净化器从开始使用到净化效率为![]() 时对颗粒物的累计净化量(单位:克).根据国家标准,对空气净化器的累计净化量(CCM)有如下等级划分:
时对颗粒物的累计净化量(单位:克).根据国家标准,对空气净化器的累计净化量(CCM)有如下等级划分:
累计净化量(克) |
|
|
| 12以上 |
等级 |
|
|
|
|
已知某批空气净化器共![]() 台,其累计净化量都分布在区间
台,其累计净化量都分布在区间![]() 内,为了解其质量,随机抽取了
内,为了解其质量,随机抽取了![]() 台净化器作为样本进行估计,按照
台净化器作为样本进行估计,按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 均匀分组,其中累计净化量在
均匀分组,其中累计净化量在![]() 的所有数据有:
的所有数据有:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 和
和![]() ,并绘制了如下频率分布直方图.
,并绘制了如下频率分布直方图.
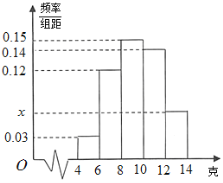
(1)求![]() 的值及频率分布直方图中
的值及频率分布直方图中![]() 的值;
的值;
(2)以样本估计总体,试估计这批空气净化器(共2000台)中等级为![]() 的空气净化器有多少台?
的空气净化器有多少台?
(3)从累计净化量在![]() 的样本中随机抽取2台,求恰好有1台等级为
的样本中随机抽取2台,求恰好有1台等级为![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】采用系统抽样方法从960人中抽取32人做问卷调查,为此将他们随即编号为1,2…960,分组后在第一组采用简单随机抽样的方法抽到的号码为5,抽到的32人中,编号落入区间[1,450]的人做问卷A,编号落入区间[451,750]的人做问卷B,其余的人做问卷C,则抽到的32人中,做问卷C的人数为( )
A.15
B.10
C.9
D.7
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() x3﹣2ax2+3x(x∈R).
x3﹣2ax2+3x(x∈R).
(1)若a=1,点P为曲线y=f(x)上的一个动点,求以点P为切点的切线斜率取最小值时的切线方程;
(2)若函数y=f(x)在(0,+∞)上为单调增函数,试求满足条件的最大整数a.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]()
(1)当a=2时,求f(x)在x∈[0,1]的最大值;
(2)当0<a<1,f(x)在x∈[0,1]上的最大值和最小值之和为a,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列{an}的前n项和为Sn , 且S4=4S2 , a2n=2an+1.
(Ⅰ)求数列{an}的通项公式
(Ⅱ)设数列{bn}的前n项和为Tn , 且 ![]() (λ为常数).令cn=b2n , (n∈N*),求数列{cn}的前n项和Rn .
(λ为常数).令cn=b2n , (n∈N*),求数列{cn}的前n项和Rn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com