
【题目】已知椭圆C:![]() (
(![]() )的一个焦点与抛物线
)的一个焦点与抛物线![]() 的焦点相同,
的焦点相同,![]() ,
,![]() 为椭圆的左、右焦点,M为椭圆上任意一点,若
为椭圆的左、右焦点,M为椭圆上任意一点,若![]() 的面积最大值为1.
的面积最大值为1.
(1)求椭圆C的方程;
(2)设不过原点的直线l:![]() 与椭圆C交于不同的两点A、B,若直线l的斜率是直线
与椭圆C交于不同的两点A、B,若直线l的斜率是直线![]() 、
、![]() 斜率的等比中项,求
斜率的等比中项,求![]() 面积的取值范围.
面积的取值范围.
 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
【题目】“石头、剪刀、布”,又称“猜丁壳”,是一种流行多年的猜拳游戏,起源于中国,然后传到日本、朝鲜等地,随着亚欧贸易的不断发展,它传到了欧洲,到了近代逐渐风靡世界.其游戏规则是:出拳之前双方齐喊口令,然后在语音刚落时同时出拳,握紧的拳头代表“石头”,食指和中指伸出代表“剪刀”,五指伸开代表“布”.“石头”胜“剪刀”、“剪刀”胜“布”、而“布”又胜过“石头”.若所出的拳相同,则为和局.小军和大明两位同学进行“五局三胜制”的“石头、剪刀、布”游戏比赛,则小军和大明比赛至第四局小军胜出的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中装有9只球,其中标有数字1,2,3,4的小球各2个,标数字5的小球有1个.从袋中任取3个小球,每个小球被取出的可能性都相等,用![]() 表示取出的3个小球上的最大数字.
表示取出的3个小球上的最大数字.
(1)求取出的3个小球上的数字互不相同的概率;
(2)求随机变量![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某篮球队员进行定点投篮训练,每次投中的概率是![]() ,且每次投篮的结果互不影响.
,且每次投篮的结果互不影响.
(1)假设这名队员投篮5次,求恰有2次投中的概率;
(2)假设这名队员投篮3次,每次投篮,投中得1分,为投中得0分,在3次投篮中,若有2次连续投中,而另外一次未投中,则额外加1分;若3次全投中,则额外加3分,记![]() 为队员投篮3次后的总的分数,求
为队员投篮3次后的总的分数,求![]() 的分布列及期望.
的分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知平面![]() 平面
平面![]() ,B为线段
,B为线段![]() 的中点,
的中点,![]() ,四边形
,四边形![]() 为正方形,平面
为正方形,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,M为棱
,M为棱![]() 的中点.
的中点.
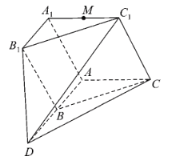
(1)若N为线段![]() 上的点,且直线
上的点,且直线![]() 平面
平面![]() ,试确定点N的位置;
,试确定点N的位置;
(2)求平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
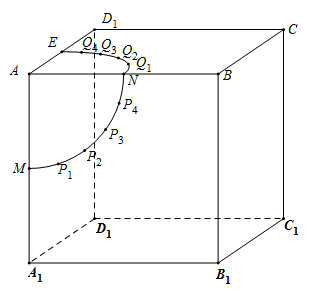
【题目】如图,棱长为2的正方体![]() 中,点
中,点![]() 分别为棱
分别为棱![]() 的中点,以
的中点,以![]() 为圆心,1为半径,分别在面
为圆心,1为半径,分别在面![]() 和面
和面![]() 内作弧
内作弧![]() 和
和![]() ,并将两弧各五等分,分点依次为
,并将两弧各五等分,分点依次为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 以及
以及![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() .一只蚂蚁欲从点
.一只蚂蚁欲从点![]() 出发,沿正方体的表面爬行至
出发,沿正方体的表面爬行至![]() ,则其爬行的最短距离为________.参考数据:
,则其爬行的最短距离为________.参考数据:![]() ;
;![]() ;
;![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com