练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知y＝f(x)在定义域(－1,1)上是减函数，且f(1－a)＜f(3a－1)，则a的取值范围是__________．

    (0，)　由题意，可得1＞1－a＞3a－1＞－1，即解得0＜a＜.

    所以a的取值范围是(0，)．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2002年全国各省市高考模拟试题汇编 题型：044

    已知：如图射线OA为y＝kx(k＞0，x＞0)，射线OB为y＝－kx(x＞0)，动点P(x，y)在∠AOx的内部，PM⊥OA于M，PN⊥OB于N，四边形ONPM的面积恰为k．

    (Ⅰ)当k为定值时，动点P的纵坐标y是其横坐标x的函数，求这个函数y＝f(x)的解析式；

    (Ⅱ)根据k的取值范围，确定y＝f(x)的定义域．

    查看答案和解析>>

    科目：高中数学 来源：宁夏银川二中2011届高三第一次月考数学理科试题 题型：022

    已知函数y＝f(x)是偶函数，y＝g(x)是奇函数，它们的定域[－π，π]，且它们在x∈[0，π]上的图象如图所示，则不等式＜0的解集是________．

    查看答案和解析>>

    科目：高中数学 来源：山东省淄博市2010届高三第二次模拟考试数学文科 题型：044

    如图，已知直线l：x＝my＋1过椭圆C：＝1的右焦点F，抛物线：x2＝4y的焦点为椭圆C的上顶点，且直线l交椭圆C于A、B两点，点A、F、B在直线g：x＝4上的射影依次为点D、K、E．

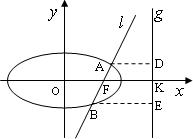
    (Ⅰ)求椭圆C的方程；

    (Ⅱ)若直线l交y轴于点M，且，当m变化时，探求λ1＋λ2的值是否为定值？若是，求出λ1＋λ2的值，否则，说明理由；

    (Ⅲ)连接AE、BD，试证明当m变化时，直线AE与BD相交于定点N．

    查看答案和解析>>

    科目：高中数学 来源：2012高三数学一轮复习单元练习题　函数与数列(2) 题型：044

    已知f(x)＝(x∈R)，P1(x1，y1)、P2(x2，y2)是函数y＝f(x)图象上两点，且线段P1P2中点P的横坐标是．

    (1)求证：点P的纵坐标是定值；

    (2)若数列{an}的通项公式是an＝f()(m∈N*，n＝1，2，…m)，求数列{an}的前m项和Sm；

    (3)在(2)的条件下，若m∈N*时，不等式恒成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：新课标2012届高三二轮复习综合验收(6)数学理科试题 题型：044

    已知椭圆C的中心在原点，焦点在x轴上，离心率等于，它的一个顶点恰好是抛物线y＝x2的焦点，

    (Ⅰ)求椭圆C的标准方程；

    (Ⅱ)过椭圆C的右焦点F作直线l交椭圆C于A、B两点，交y轴于M点，若＝λ1，＝λ2，求证：λ1＋λ2为定值．

    查看答案和解析>>

    同步练习册答案