
【题目】已知数列{an}的各项均为正数,Sn是数列{an}的前n项和,且4Sn=an2+2an﹣3.
(1)求数列{an}的通项公式;
(2)已知bn=2n,求Tn=a1b1+a2b2+…+anbn的值.
【答案】(1)an=3+2(n﹣1)=2n+1;
(2)(2n﹣1)2n+2.
【解析】试题分析:(1)由题意知![]() ,解得a1=3,由此能够推出数列{an}是以3为首项,2为公差的等差数列,所以an=3+2(n﹣1)=2n+1.
,解得a1=3,由此能够推出数列{an}是以3为首项,2为公差的等差数列,所以an=3+2(n﹣1)=2n+1.
(2)由题意知Tn=3×21+5×22+…+(2n+1)2n,2Tn=3×22+5×23+(2n﹣1)2n+(2n+1)2n+1,二者相减可得到Tn=a1b1+a2b2+…+anbn的值.
解:(1)当n=1时,![]() ,解出a1=3,
,解出a1=3,
又4Sn=an2+2an﹣3①
当n≥2时4sn﹣1=an﹣12+2an﹣1﹣3②
①﹣②4an=an2﹣an﹣12+2(an﹣an﹣1),即an2﹣an﹣12﹣2(an+an﹣1)=0,
∴(an+an﹣1)(an﹣an﹣1﹣2)=0,
∵an+an﹣1>0∴an﹣an﹣1=2(n≥2),
∴数列{an}是以3为首项,2为公差的等差数列,∴an=3+2(n﹣1)=2n+1.
(2)Tn=3×21+5×22+…+(2n+1)2n③
又2Tn=3×22+5×23+(2n﹣1)2n+(2n+1)2n+1④
④﹣③Tn=﹣3×21﹣2(22+23++2n)+(2n+1)2n+1﹣6+8﹣22n﹣1+(2n+1)2n+1=(2n﹣1)2n+2


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:高中数学 来源: 题型:
【题目】随着社会的发展,终身学习成为必要,工人知识要更新,学习培训必不可少,现某工厂有工人1000名,其中250名工人参加短期培训(称为![]() 类工人),另外750名工人参加过长期培训(称为
类工人),另外750名工人参加过长期培训(称为![]() 类工人),从该工厂的工人中共抽查了100名工人,调查他们的生产能力(此处生产能力指一天加工的零件数)得到
类工人),从该工厂的工人中共抽查了100名工人,调查他们的生产能力(此处生产能力指一天加工的零件数)得到![]() 类工人生产能力的茎叶图(左图),
类工人生产能力的茎叶图(左图),![]() 类工人生产能力的频率分布直方图(右图).
类工人生产能力的频率分布直方图(右图).

(1)问![]() 类、
类、![]() 类工人各抽查了多少工人,并求出直方图中的
类工人各抽查了多少工人,并求出直方图中的![]() ;
;
(2)求![]() 类工人生产能力的中位数,并估计
类工人生产能力的中位数,并估计![]() 类工人生产能力的平均数(同一组中的数据用该组区间的中点值作代表);
类工人生产能力的平均数(同一组中的数据用该组区间的中点值作代表);
(3)若规定生产能力在![]() 内为能力优秀,由以上统计数据在答题卡上完成下面的
内为能力优秀,由以上统计数据在答题卡上完成下面的![]() 列联表,并判断是否可以在犯错误概率不超过0.1%的前提下,认为生产能力与培训时间长短有关.能力与培训时间列联表
列联表,并判断是否可以在犯错误概率不超过0.1%的前提下,认为生产能力与培训时间长短有关.能力与培训时间列联表
短期培训 | 长期培训 | 合计 | |
能力优秀 | |||
能力不优秀 | |||
合计 |
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高三理科某班有男同学30名,女同学15名,老师按照分层抽样的方法组建一个6人的课外兴趣小组.
(1)求课外兴趣小组中男、女同学各应抽取的人数;
(2)在一周的技能培训后从这6人中选出两名同学做某项实验,方法是先从小组里选出1名同学做实验,该同学做完后,再从小组内剩下的同学中选1名同学做实验,求选出的两名同学中恰好仅有一名女同学的概率;
(3)实验结束后,第一次做实验的同学得到的实验数据为1.6、2、1.9、2.5、2,第二次做实验的同学得到的实验数据是2.1、1.8、1.9、2、2.2,请问哪位同学的实验更稳定?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(ax2+bx+c)ex(a>0)的导函数y=f′(x)的两个零点为-3和0.
(1)求f(x)的单调区间;
(2)若f(x)的极小值为-1,求f(x)的极大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=kex﹣x3+2 (k∈R)恰有三个极值点xl,x2,x3,且xl<x2<x3.
(I)求k的取值范围:
(II)求f(x2)的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 且
且![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 垂直.
垂直.
(1)求实数![]() 值;
值;
(2)若不等式![]() 对任意的实数
对任意的实数![]() 及
及![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)设![]() ,且数列
,且数列![]() 的前
的前![]() 项和为
项和为![]() ,求证:
,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,以
中,以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的方程是
的方程是![]() ,将
,将![]() 向上平移2个单位得到曲线
向上平移2个单位得到曲线![]() .
.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)直线![]() 的参数方程为
的参数方程为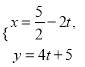 (
(![]() 为参数),判断直线
为参数),判断直线![]() 与曲线
与曲线![]() 的位置关系.
的位置关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系内,已知点![]() 及线段
及线段![]() ,在线段
,在线段![]() 上任取一点
上任取一点![]() ,线段
,线段![]() 长度的最小值称为“点
长度的最小值称为“点![]() 到线段
到线段![]() 的距离”,记为
的距离”,记为![]() .
.
(1)设点![]() ,线段
,线段![]()
![]() ,求
,求![]() ;
;
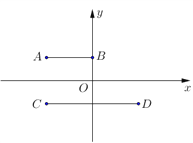
(2)设![]() ,
, ![]() ,
, ![]() ,
, ![]() ,线段
,线段![]() ,线段
,线段![]() ,若点
,若点![]() 满足
满足![]() ,求
,求![]() 关于
关于![]() 的函数解析式,并写出该函数的值域.
的函数解析式,并写出该函数的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com