
【题目】已知函数
(1)证明:![]() 在
在![]() 上单调递减;
上单调递减;
(2)已知![]() 在
在![]() 单调递增,记函数
单调递增,记函数![]() 的最小值为
的最小值为![]() .
.
①求![]() 的表达式;
的表达式;
②求![]() 的最大值.
的最大值.
【答案】(1)见解析;(2)①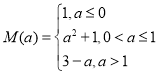 ;②2.
;②2.
【解析】
(1)直接利用单调性的定义证明;
(2)①先求得函数![]() 在
在![]() 时的最小值,再看当
时的最小值,再看当![]() 时,函数
时,函数![]() 的最小值,只需对a讨论,借助于二次函数的单调性求得答案.
的最小值,只需对a讨论,借助于二次函数的单调性求得答案.
②直接由解析式得解.
(1)任取x1,x2∈(0,1),设x1<x2,则
f(x1)﹣f(x2)=![]()
![]()
 .
.
∵0<x1<x2<1,∴![]() ,∴
,∴![]() <2,
<2,
∴ 0,即f(x1)﹣f(x2)>0,
0,即f(x1)﹣f(x2)>0,
∴f(x1)>f(x2).
∴函数f(x)在(0,1)上单调递减;
(2)①∵![]() 在
在![]() 单调递增,∴函数
单调递增,∴函数![]() 在
在![]() 时满足在(0,1)上单调递减,在
时满足在(0,1)上单调递减,在![]() 单调递增,此时在
单调递增,此时在![]() 时的最小值为
时的最小值为![]() ,
,
当![]() 时,
时,![]() 对称轴为
对称轴为![]() ,
,
当![]() 时,二次函数开口向上,
时,二次函数开口向上,![]() ;
;
当a>0时,函数![]() 在
在![]() 时单调递减,函数
时单调递减,函数![]() 在
在![]() 时
时![]() .
.
当![]() 时,即a>1时,
时,即a>1时,![]() ,
,
当![]() <a≤
<a≤![]() 时,
时,![]() ,
,
综上, ;
;
②由 ,可得当a=1时,函数
,可得当a=1时,函数![]() 有最大值为
有最大值为![]() .
.


科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
①映射不一定是函数,但函数一定是其定义域到值域的映射;
②函数![]() 的反函数是
的反函数是![]() ,则
,则![]() ;
;
③函数![]() 的最小值是
的最小值是![]() ;
;
④对于函数![]() ,则
,则![]() 既是奇函数又是偶函数.
既是奇函数又是偶函数.
其中所有正确命题的序号是( ).
A.①③B.②③C.①③④D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出函数![]() 如下表,则f〔g(x)〕的值域为( )
如下表,则f〔g(x)〕的值域为( )
x | 1 | 2 | 3 | 4 |
g(x) | 1 | 1 | 3 | 3 |
x | 1 | 2 | 3 | 4 |
f(x) | 4 | 3 | 2 | 1 |
A. {4,2} B. {1,3} C. {1,2,3,4} D. 以上情况都有可能
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,过点
,过点![]() 作抛物线
作抛物线![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,直线
,直线![]() 的斜率为2.
的斜率为2.
(1)求抛物线的标准方程;
(2)与圆![]() 相切的直线
相切的直线![]() ,与抛物线交于
,与抛物线交于![]() 两点,若在抛物线上存在点
两点,若在抛物线上存在点![]() ,使
,使![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年是中国改革开放40周年,改革开放40年来,从开启新时期到跨入新世纪,从站上新起点到进人新时代,我们党引领人民绘就了一幅波澜壮阔、气势恢宏的历史画卷,谱写了一曲感天动地、气壮山河的奋斗赞歌,40年来我们始终坚持保护环境和节约资源,坚持推进生态文明建设,郑州市政府也越来越重视生态系统的重建和维护,若市财政下拨一项专款100百万元,分别用于植绿护绿和处理污染两个生态维护项目,植绿护绿项目五年内带来的生态收益可表示为投放资金x(单位:百万元)的函数M(x(单位:百万元):![]() ,处理污染项目五年内带来的生态收益可表示为投放资金x(单位:百万元)的函数N(x)(单位:百万元):
,处理污染项目五年内带来的生态收益可表示为投放资金x(单位:百万元)的函数N(x)(单位:百万元):![]() .
.
(Ⅰ)设分配给植绿护绿项目的资金为x(百万元),则两个生态项目五年内带来的收益总和为y,写出y关于x的函数解析式和定义域。
(Ⅱ)生态项目的投资开始利润薄弱,只有持之以恒,才能功在当代,利在千秋,试求出y的最大值,并求出此时对两个生态项目的投资分别为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足:
满足:![]() ,
,![]()
![]() . (其中
. (其中![]() 为自然对数的底数,
为自然对数的底数,![]() )
)
(Ⅰ)证明:![]() ;
;
(Ⅱ)设![]() ,是否存在实数
,是否存在实数![]() ,使得
,使得![]() 对任意
对任意![]() 成立?若存在,求出
成立?若存在,求出![]() 的一个值;若不存在,请说明理由.
的一个值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某粮油超市每月按出厂价30元/袋购进种大米,根据以往的统计数据,若零售价定为42元/袋,每月可销售320袋.现为了促销,经调查,若零售价每降低一元,则每月可多销售40袋.在每月的进货都销售完的前提下,零售价定为多少元/袋以及每月购进多少袋大米,超市可获得最大利润,并求出最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com