设圆C1的方程为(x+2)2+(y-3m-2)2=4m2,直线l的方程为y=x+m+2.
(1)若m=1,求圆C1上的点到直线l距离的最小值;
(2)求C1关于l对称的圆C2的方程;
(3)当m变化且m≠0时,求证:C2的圆心在一条定直线上,并求C2所表示的一系列圆的公切线方程.
【答案】
分析:(1)把m=1代入圆的方程和直线l的方程,分别确定出解析式,然后利用点到直线的距离公式求出圆心到直线l的距离d,发现d大于半径r,故直线与圆的位置关系是相离,则圆上的点到直线l距离的最小值为d-r,求出值即可;
(2)由圆的方程找出圆心坐标,设出圆心关于直线l的对称点的坐标,由直线l的斜率,根据两直线垂直时斜率的乘积为-1求出直线C
1C
2的斜率,由圆心及对称点的坐标表示出斜率,等于求出的斜率列出一个关系式,然后利用中点坐标公式,求出两圆心的中点坐标,代入直线l的方程,得到另一个关系式,两关系式联立即可用m表示出a与b,把表示出的a与b代入圆C
2的方程即可;
(3)由表示出的a与b消去m,得到a与b的关系式,进而得到圆C
2的圆心在定直线x-2y=0上;分公切线的斜率不存在和存在两种情况考虑,当公切线斜率不存在时,容易得到公切线方程为x=0;当公切线斜率存在时,设直线y=kx+b与圆系中的所有圆都相切,根据点到直线的距离公式表示出圆心(a,b)到直线y=kx+b的距离d,当d等于圆的半径2|m|,化简后根据多项式为0时各项的系数为0,即可求出k与b的值,从而确定出C
2所表示的一系列圆的公切线方程,综上,得到所有C
2所表示的一系列圆的公切线方程.
解答:解:(1)∵m=1,∴圆C
1的方程为(x+2)
2+(y-5)
2=4,直线l的方程为x-y+3=0,
所以圆心(-2,5)到直线l距离为:
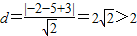
,
所以圆C
1上的点到直线l距离的最小值为
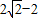
;(4分)
(2)圆C
1的圆心为C
1(-2,3m+2),设C
1关于直线l对称点为C
2(a,b),
则
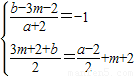
解得:
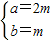
,
∴圆C
2的方程为(x-2m)
2+(y-m)
2=4m
2;
(3)由
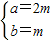
消去m得a-2b=0,
即圆C
2的圆心在定直线x-2y=0上.(9分)
①当公切线的斜率不存在时,易求公切线的方程为x=0;
②当公切线的斜率存在时,设直线y=kx+b与圆系中的所有圆都相切,
则
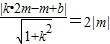
,即(-4k-3)m
2+2(2k-1)•b•m+b
2=0,
∵直线y=kx+b与圆系中的所有圆都相切,所以上述方程对所有的m值都成立,
所以有:
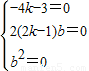
解之得:
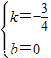
,
所以C
2所表示的一系列圆的公切线方程为:
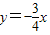
,
故所求圆的公切线为x=0或
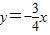
.(14分)
点评:此题考查了直线与圆的位置关系,以及关于点与直线对称的圆的方程.此题的综合性比较强,要求学生审清题意,综合运用方程与函数的关系,掌握直线与圆相切时圆心到直线的距离等于半径,在作(3)时先用消去参数的方法求定直线的方程,然后采用分类讨论的数学思想分别求出C
2所表示的一系列圆的公切线方程.

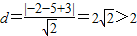 ,
,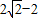 ;(4分)
;(4分)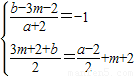 解得:
解得: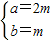 ,
,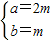 消去m得a-2b=0,
消去m得a-2b=0,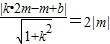 ,即(-4k-3)m2+2(2k-1)•b•m+b2=0,
,即(-4k-3)m2+2(2k-1)•b•m+b2=0,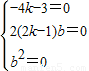 解之得:
解之得: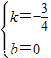 ,
,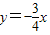 ,
,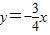 .(14分)
.(14分)

 名校课堂系列答案
名校课堂系列答案