
【题目】若对任意的x∈[﹣1,2],都有x2﹣2x+a≤0(a为常数),则a的取值范围是( )
A.(﹣∞,﹣3]
B.(﹣∞,0]
C.[1,+∞)
D.(﹣∞,1]
科目:高中数学 来源: 题型:
【题目】已知f(x)为定义在[﹣1,1]上的奇函数,当x∈[﹣1,0]时,函数解析式为 ![]() .
.
(1)求f(x)在[0,1]上的解析式;
(2)求f(x)在[0,1]上的最值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a>0且满足不等式22a+1>25a﹣2 .
(1)求实数a的取值范围.
(2)求不等式loga(3x+1)<loga(7﹣5x).
(3)若函数y=loga(2x﹣1)在区间[1,3]有最小值为﹣2,求实数a值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .若点
.若点![]() 在椭圆
在椭圆![]() 上,则点
上,则点![]() 称为点
称为点![]() 的一个“椭点”.
的一个“椭点”.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() :
: ![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
, ![]() 两点,且
两点,且![]() ,
, ![]() 两点的“椭点”分别为
两点的“椭点”分别为![]() ,
, ![]() ,以
,以![]() 为直径的圆经过坐标原点,试求
为直径的圆经过坐标原点,试求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究所计划利用“神七”宇宙飞船进行新产品搭载实验,计划搭载新产品A、B,要根据该产品的研制成本、产品重量、搭载实验费用和预计产生收益来决定具体安排,通过调查,有关数据如表:
产品A(件) | 产品B(件) | ||
研制成本、搭载费用之和(万元) | 20 | 30 | 计划最大资金额300万元 |
产品重量(千克) | 10 | 5 | 最大搭载重量110千克 |
预计收益(万元) | 80 | 60 |
试问:如何安排这两种产品的件数进行搭载,才能使总预计收益达到最大,最大收益是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,以原点O为圆心,椭圆的短半轴长为半径的圆与直线x﹣y+
,以原点O为圆心,椭圆的短半轴长为半径的圆与直线x﹣y+ ![]() =0相切.
=0相切.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若直线L:y=kx+m与椭圆C相交于A、B两点,且kOAkOB=﹣ ![]() ,求证:△AOB的面积为定值.
,求证:△AOB的面积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
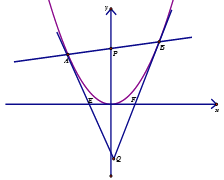
【题目】已知抛物线C: ![]() ,过点
,过点![]() 的动直线l与C相交于
的动直线l与C相交于![]() 两点,抛物线C在点A和点B处的切线相交于点Q.
两点,抛物线C在点A和点B处的切线相交于点Q.
(Ⅰ)写出抛物线的焦点坐标和准线方程;
(Ⅱ)求证:点Q在直线![]() 上;
上;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com