箱子中装有6张卡片,分别写有1到6这6个整数.从箱子中任意取出一张卡片,记下它的读数x,然后放回箱子,第二次再从箱子中取出一张卡片,记下它的读数y,试求:
(Ⅰ)x+y是5的倍数的概率;
(Ⅱ)x-y是3的倍数的概率;
(Ⅲ)x,y中至少有一个5或6的概率.
【答案】
分析:(Ⅰ)所有的实数对(x,y)共有6×6=36个,用列举法求得其中满足x+y是5的倍数的实数对有7个,由此求得故x+y
是5的倍数的概率.
(Ⅱ)用列举法求得满足x-y是3的倍数的实数对有12个,由此求得x-y是3的倍数的概率.
(Ⅲ) 用列举法求得x,y中至少有一个5或6的实数对共有19个,由此求得 x,y中至少有一个5或6的概率.
解答:解:(Ⅰ)所有的实数对(x,y)共有6×6=36个,满足x+y是5的倍数的实数对有(1,4)、(4,1)、(2,3)、
(3,2)、(5,5),(4,6)、(6,4)共有7个,
故x+y是5的倍数的概率等于

.
(Ⅱ)满足x-y是3的倍数的实数对有(4,1)、(5,2)、(6,3)、(1,1)、(2,2)、(3,3)、(4,4)、(5,5)、(6,6),(1,4)、(2,5)、(3,6),共有12个,故x-y是3的倍数的概率等于
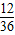
=

.
(Ⅲ) x,y中至少有一个5或6的实数对有(1,5)、(5,1)、(2,5)、(5,2)、(3,5)、(5,3)、
(4,5)、(5,4)、(5,5)(5,6)、(6,5)、(6,4)、(4,6)、(3,6)、(6,3)、(2,6)、
(6,2)、(1,6)、(6,1),(6,6)共有 20个,
故 x,y中至少有一个5或6的概率等于

=

.
点评:本题主要考查用列举法计算可以列举出基本事件和满足条件的事件的概率,应用列举法来解题,是这一部分的最主要
思想,属于基础题.

 .
.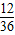 =
= .
. =
= .
.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案