
【题目】已知![]() 、
、![]() 分别是离心率为
分别是离心率为![]() 的椭圆
的椭圆![]() :
:![]() 的左、右焦点,点
的左、右焦点,点![]() 是椭圆
是椭圆![]() 上异于其左、右顶点的任意一点,过右焦点
上异于其左、右顶点的任意一点,过右焦点![]() 作
作![]() 的外角平分线
的外角平分线![]() 的垂线
的垂线![]() ,交
,交![]() 于点
于点![]() ,且
,且![]() (
(![]() 为坐标原点).
为坐标原点).
(1)求椭圆![]() 的方程;
的方程;
(2)若点![]() 在圆
在圆![]() 上,且在第一象限,过
上,且在第一象限,过![]() 作圆
作圆![]() 的切线交椭圆于
的切线交椭圆于![]() 、
、![]() 两点,问:
两点,问:![]() 的周长是否为定值?如果是,求出该定值;如果不是,说明理由.
的周长是否为定值?如果是,求出该定值;如果不是,说明理由.
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:高中数学 来源: 题型:
【题目】下列命题说法中正确的是
A. 对于实数![]() ,“
,“![]() ”是
”是![]() 或
或![]() 的充分不必要条件
的充分不必要条件
B. 已知![]() 都是整数,则命题“若
都是整数,则命题“若![]() ,则
,则![]() 不都是奇数”是假命题
不都是奇数”是假命题
C. “若![]() ,则关于
,则关于![]() 的方程
的方程![]() 有实根”的逆否命题为假命题
有实根”的逆否命题为假命题
D. 命题“全等三角形的面积相等”的否命题为真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)已知四棱锥![]() 的侧棱长与底面边长都相等,四边形
的侧棱长与底面边长都相等,四边形![]() 为正方形,点
为正方形,点![]() 是
是![]() 的中点,求异面直线
的中点,求异面直线![]() 与
与![]() 所成角的余弦值.
所成角的余弦值.

(2)如图,在长方体![]() 中,
中,![]() 分别是
分别是![]() 的中点,求异面直线
的中点,求异面直线![]() 与
与![]() 所成角的余弦值.
所成角的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了治理大气污染,某市2017年初采用了一系列措施,比如“煤改电”,“煤改气”,“整治散落污染企业”等.下表是该市2016年11月份和2017年11月份的空气质量指数(![]() )(
)(![]() 指数越小,空气质量越好)统计表.根据表中数据回答下列问题:
指数越小,空气质量越好)统计表.根据表中数据回答下列问题:
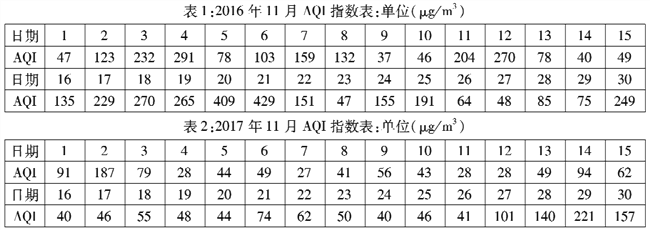
(1)将2017年11月的空气质量指数![]() 数据用该天的对应日期作为样本编号,再用系统抽样方法从中抽取6个
数据用该天的对应日期作为样本编号,再用系统抽样方法从中抽取6个![]() 数据,若在2017年11月16日到11月20日这五天中用简单随机抽样抽取到的样本的编号是19号,写出抽出的样本数据;
数据,若在2017年11月16日到11月20日这五天中用简单随机抽样抽取到的样本的编号是19号,写出抽出的样本数据;
(2)从(1)中抽出的6个样本数据中随机抽取2个,求这2个![]() 数据之差的绝对值小于30的概率;
数据之差的绝对值小于30的概率;
(3)根据《环境空气质量指数(![]() )技术规定(试行)》规定:当空气质量指数为
)技术规定(试行)》规定:当空气质量指数为![]() (含50)时,空气质量级别为一级,求出这两年11月空气质量指数为一级的概率,你认为该市2017年初开始采取的这些大气污染治理措施是否有效?
(含50)时,空气质量级别为一级,求出这两年11月空气质量指数为一级的概率,你认为该市2017年初开始采取的这些大气污染治理措施是否有效?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】按照国家质量标准:某种工业产品的质量指标值落在[100,120)内,则为合格品,否则为不合格品.某企业有甲乙两套设备生产这种产品,为了检测这两套设备的生产质量情况,随机从两套设备生产的大量产品中各抽取了50件产品作为样本对规定的质量指标值进行检测.表1是甲套设备的样本频数分布表,图1是乙套设备的样本频率分布直方图.

质量指标值 | [95,100) | [100,105) | [105,110) | [110,115) | [115,120) | [120,125] |
频数 | 1 | 4 | 19 | 20 | 5 | 1 |
表1:甲套设备的样本频数分布表
(1)将频率视为概率,若乙套设备生产了5000件产品,则其中合格品约有多少件?
(2)填写下面2×2列联表,并根据列联表判断是否有95%的把握认为这种产品的质量指标值与甲乙两套设备的选择有关:
甲套设备 | 乙套设备 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
(3)根据表和图,对甲、乙两套设备的优劣进行比较.参考公式及数据:x2=![]()
P(Х2≥k) | 0.100 | 0.050 | 0.010 |
k | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的直角顶点
的直角顶点![]() 在
在![]() 轴上,点
轴上,点![]() ,
,![]() 为斜边
为斜边![]() 的中点,且
的中点,且![]() 平行于
平行于![]() 轴.
轴.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)设点![]() 的轨迹为曲线
的轨迹为曲线![]() ,直线
,直线![]() 与
与![]() 的另一个交点为
的另一个交点为![]() .以
.以![]() 为直径的圆交
为直径的圆交![]() 轴于
轴于![]() 、
、![]() ,记此圆的圆心为
,记此圆的圆心为![]() ,
,![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() ’(
’(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 和
和![]() 的直角坐标方程;
的直角坐标方程;
(2)已知直线![]() 与
与![]() 轴交于点
轴交于点![]() ,且与曲线
,且与曲线![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com