
分析 令t=sinx+cosx=$\sqrt{2}sin(x+\frac{π}{4})$,求出t的范围,然后分段作出g(t)=$\frac{{t}^{2}-1}{2}$的图象,最后结合$[\frac{{t}^{2}-1}{2}]$与[t]求得答案.
解答 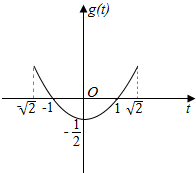 解:令t=sinx+cosx=$\sqrt{2}sin(x+\frac{π}{4})$,
解:令t=sinx+cosx=$\sqrt{2}sin(x+\frac{π}{4})$,
则t∈[$-\sqrt{2},\sqrt{2}$],
再由t=sinx+cosx,得t2=1+2sinxcosx,
∴sinx•cosx=$\frac{{t}^{2}-1}{2}$.
∴y=f(t)=[sinx•cos]+[sinx+cosx]=$[\frac{{t}^{2}-1}{2}]+[t]$($-\sqrt{2}≤t≤\sqrt{2}$).
如图:
当t∈$[-\sqrt{2},-1)$时,$\frac{{t}^{2}-1}{2}$∈(0,$\frac{1}{2}$],
∴y=f(t)=$[\frac{{t}^{2}-1}{2}]+[t]$=-2;
当t=-1时,$\frac{{t}^{2}-1}{2}$=0,
∴y=f(t)=$[\frac{{t}^{2}-1}{2}]+[t]$=-1;
当t∈(-1,0)时,$\frac{{t}^{2}-1}{2}$∈(-$\frac{1}{2}$,0),
∴y=f(t)=$[\frac{{t}^{2}-1}{2}]+[t]$=-2;
当t=0时,$\frac{{t}^{2}-1}{2}$=$-\frac{1}{2}$,
∴y=f(t)=$[\frac{{t}^{2}-1}{2}]+[t]$=-1;
当t∈(0,1)时,$\frac{{t}^{2}-1}{2}$∈($-\frac{1}{2}$,0),
∴y=f(t)=$[\frac{{t}^{2}-1}{2}]+[t]$=-1;
当t∈[1,$\sqrt{2}$]时,$\frac{{t}^{2}-1}{2}$∈(0,$\frac{1}{2}$],
∴y=f(t)=$[\frac{{t}^{2}-1}{2}]+[t]$=1.
∴y=[sinx•cos]+[sinx+cosx]的值域为{-2,-1,1}.
故答案为:{-2,-1,1}.
点评 本题是在新定义下对函数值域的考查,作出图形,正确分段是解答该题的关键,是中档题,但易出错.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
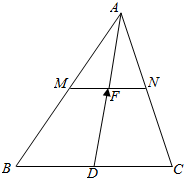 在△ABC中,已知A(7,8),B(3,5),C(4,3),M,N,D分别是AB,AC,BC的中点,且MN与AD交于点F,求$\overrightarrow{DF}$的坐标.
在△ABC中,已知A(7,8),B(3,5),C(4,3),M,N,D分别是AB,AC,BC的中点,且MN与AD交于点F,求$\overrightarrow{DF}$的坐标.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0<x0<$\frac{1}{2}$ | B. | $\frac{1}{2}$<x0<1 | C. | $\frac{\sqrt{2}}{2}$<x0<$\sqrt{2}$ | D. | $\sqrt{2}$<x0$<\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com