【题目】已知圆C的方程为(x－1)2＋y2＝9，求过M(－2,4)的圆C的切线方程．
【答案】.圆C的切线方程为x＋2＝0或7x＋24y－82＝0.
【解析】试题解析：先判断点M(－2,4)在圆C外，故可作两条切线，然后根据待定系数法求直线方程，解题中分两种情况，即切线的斜率存在和不存在。
试题解析：
因为r＝3，圆心C(1,0)到点M(－2,4)的距离d＝5>r，
所以点M(－2,4)在圆C外，切线有两条．
(1)当切线的斜率存在时，设过点M(－2,4)的圆C的切线方程为y－4＝k(x＋2)，
即kx－y＋2k＋4＝0.
由圆心C(1,0)到切线的距离等于半径3，
得
＝3.
解得k＝－
，
所以线方程得7x＋24y－82＝0.
(2)当切线的斜率不存在时，圆心C(1,0)到直线x＝－2的距离等于半径3，
所以x＝－2也是圆C的切线方程．
综上所求圆C的切线方程为x＋2＝0或7x＋24y－82＝0.
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】知f（x）是定义在R上的奇函数，且当x∈（0，+∞）时，f（x）=2018x+log2018x，则函数f（x）的零点个数是（ ）
A.1
B.2
C.3
D.4
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知三棱柱ABC-A′B′C′，底面是边长为1的正三角形，侧面为全等的矩形且高为8，求一点自A点出发沿着三棱柱的侧面绕行一周后到达A′点的最短路线长.
本题条件不变，求一点自A点出发沿着三棱柱的侧面绕行两周后到达A′点的最短路线长.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知直线l1：(k－3)x＋(4－k)y＋1＝0与l2：2(k－3)x－2y＋3＝0.
(1)若这两条直线垂直，求k的值；
(2)若这两条直线平行，求k的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】长方体ABCD－A1B1C1D1中，AB＝BC＝2，D1D＝3，点M是B1C1的中点，点N是AB的中点．建立如图所示的空间直角坐标系.
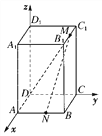
(1)写出点D、N、M的坐标；
(2)求线段MD、MN的长度．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列说法正确的是（ ）
A.x，y∈R，若x+y≠0，则x≠1且y≠﹣1
B.a∈R，“ 
＜1“是“a＞1“的必要不充分条件
C.命题“x∈R，使得x2+2x+3＜0”的否定是“x∈R，都有x2+2x+3＞0”
D.“若am2＜bm2 ， 则a＜b”的逆命题为真命题
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图1，在Rt△ABC中，∠C=90°，BC=6，AC=3，D，E分别是AC，AB上的点，且DE∥BC，DE=4，将△ADE沿DE折起到△A1DE的位置，使A1C⊥CD，如图2．
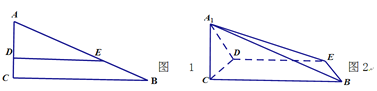
（1）求证：
平面
；
（2）过点E作截面
平面
，分别交CB于F，
于H，求截面的面积。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
