
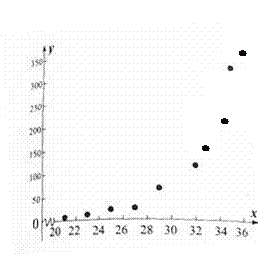
����Ŀ�����۲⣬ij����IJ�����y���¶�x�йأ��ֽ��ռ������¶�xi�Ͳ�����yi��i=1��2������10����10��۲��������˳����������õ�����ͼ��ɢ��ͼ��һЩͳ��������
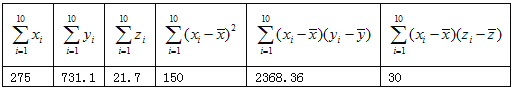
����![]() ,
, ![]()
��1������ɢ��ͼ�жϣ� ![]() ,
, ![]() ��
��![]() ��һ��������Ϊy��x֮��Ļع鷽��ģ�ͣ��������жϼ��ɣ�����˵�����ɣ�
��һ��������Ϊy��x֮��Ļع鷽��ģ�ͣ��������жϼ��ɣ�����˵�����ɣ�
��2�����ݣ�1�����жϽ�����������ݣ�
������y����x�ع鷽�̣�
����֪���˹�����������ijɱ�h��x�����¶�x�Ͳ�����y�Ĺ�ϵΪh��x��=x��lny��2.4��+170�����¶�x��xȡ������Ϊ��ֵʱ�������ɱ���Ԥ��ֵ��С��
��������һ�����ݣ�u1��v1������u2��v2��������un��vn������ع�ֱ��v=��+��u��б�ʺͽؾ����С���˹��Ʒֱ�Ϊ��=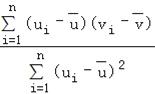 ����=
����=![]() ����
����![]() ��
��
���𰸡���1��![]() ����2��������.
����2��������.
����������������1������ɢ��ͼ�жϣ�����������ֲ���һ��ָ����������Χ���ɵý��ۣ�
��2�����ɱ任���������ֲ���һ��ֱ�߸�������˿��������Իع鷽������ϣ��������y��x�Ļع鷽����
������ת��Ϊ���κ�������ֵ���⣬��϶��κ�����ͼ�������ʿɵý��ۣ�
��⣺��1������ɢ��ͼ�жϣ�����������ֲ���һ��ָ����������Χ������![]() ������Ϊy��x֮��Ļع鷽��ģ�ͣ�
������Ϊy��x֮��Ļع鷽��ģ�ͣ�
��2���� ��z=lny �� ![]()
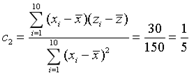
![]()
![]()
![]()
��![]()
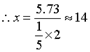 ʱ�������ɱ���Ԥ��ֵ��С��
ʱ�������ɱ���Ԥ��ֵ��С��


 ������ѧ��ʱ��ҵϵ�д�
������ѧ��ʱ��ҵϵ�д� ���������ʱ��ѵϵ�д�
���������ʱ��ѵϵ�д� �㽭�¿γ���άĿ�������ʱ��ѵϵ�д�
�㽭�¿γ���άĿ�������ʱ��ѵϵ�д� ��������ϵ�д�
��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ѧ���Ŀ����Ķ�ʱ�������ijѧУ�����ȡ��50�˽���ͳ�Ʒ���������50��ÿ���Ķ���ʱ�䣨��λ�����ӣ����Ƴ�Ƶ���ֲ��������±���ʾ��
�Ķ�ʱ�� | [0,20�� | [20,40�� | [40,60�� | [60,80�� | [80,100�� | [100,120] |
���� | 8 | 10 | 12 | 11 | 7 | 2 |
����ÿ���Ķ�ʱ����60�������ϣ���60���ӣ���ͬѧ��Ϊ���Ķ����ˡ�������ͳ�ƽ������Ů���Ķ����˵����ݣ���������ͼ��ʾ�ĵȸ�����ͼ��

��1��������֪�������2x2������;
���� | Ů�� | �ܼ� | |
�Ķ����� | |||
���Ķ����� | |||
�ܼ� |
��2�����ж��Ƿ���![]() �İ�����Ϊ���Ķ����ˡ����Ա��йأ�
�İ�����Ϊ���Ķ����ˡ����Ա��йأ�
�����ο���ʽ![]()
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����й��ڻع������˵���д�������� ����
(1). �в�ͼ�вв�����ڵ�ˮƽ��״����Խ������ع鷽�̵�Ԥ����ȷ��Խ��.
(2). �ع�ֱ��һ������������![]() ��
��
(3). ����ģ���вв�ƽ����ԽС��ģ����ϵ�Ч��Խ����
(4) .�ס�������ģ�͵�![]() �ֱ�ԼΪ0.88��0.80����ģ���ҵ����Ч������.
�ֱ�ԼΪ0.88��0.80����ģ���ҵ����Ч������.
A. 4 B. 3 C. 2 D. 1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() �Ƕ�����
�Ƕ�����![]() �ϵ��溯������
�ϵ��溯������![]() ����a��
����a��![]() ��
��![]() ʱ����
ʱ����![]() ������
������
![]() ��
��![]() ��
��![]() ������
������![]() 1�ϵ����ֵ��
1�ϵ����ֵ��
![]() ��
��![]() ���������
���������![]() ����
����![]() ����ʵ��m��ȡֵ��Χ��
����ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����Ǧ���l����Ϊ60�㣬AB����AB��l��AΪ���㣬CD�£�C��l����ACD=135�㣬������ֱ��AB��CD���ɽǵ�����ֵΪ�� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ȱ�����{an}������˵��һ����ȷ���ǣ� ��
A.a1 �� a3 �� a9�ɵȱ�����
B.a2 �� a3 �� a6�ɵȱ�����
C.a2 �� a4 �� a8�ɵȱ�����
D.a3 �� a6 �� a9�ɵȱ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ������
������![]() Ϊ�߳�Ϊ2���������Σ�����
Ϊ�߳�Ϊ2���������Σ�����![]() ,
,![]()
��1����֤��![]() ��
��
��2����![]() �㵽ƽ��
�㵽ƽ��![]() �ľ��룮
�ľ��룮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������һֱ����в���ǵ����ij������������Ϊ���о������в�����ֳ����![]() ��������ʱ��
��������ʱ��![]() ���죩�仯�Ĺ��ɣ��ռ��������£�
���죩�仯�Ĺ��ɣ��ռ��������£�
���� | 1 | 2 | 3 | 4 | 5 | 6 |
��ֳ���� | 6 | 12 | 25 | 49 | 95 | 190 |
����ɢ��ͼ�ɿ���������ֲ���һ��ָ���ͺ���![]() ����Χ.
����Χ.
����С�������λ���IJο����ݣ�
![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ������
������![]()
��1�����![]() ����
����![]() �Ļع鷽�̣�����С�������λ���֣���
�Ļع鷽�̣�����С�������λ���֣���
��2����֪![]() �����������IJв�.
�����������IJв�.
�ο���ʽ��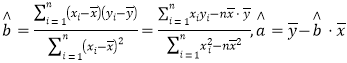
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Բ ![]() +
+ ![]() =1��a��b��0�������ҽ���ֱ�ΪF1��F2 �� �Ҷ���ΪA���϶���ΪB����֪|AB|=
=1��a��b��0�������ҽ���ֱ�ΪF1��F2 �� �Ҷ���ΪA���϶���ΪB����֪|AB|= ![]() |F1F2|��
|F1F2|��
��1������Բ�������ʣ�
��2����PΪ��Բ�������䶥���һ�㣬���߶�PBΪֱ����Բ������F1 �� ����ԭ��O��ֱ��l���Բ���У���ֱ��l��б�ʣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com