(本小题满分14分)
已知关于x的函数
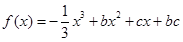
,其导函数
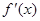
.
(1)如果函数

试确定b、c的值;
(2)设当
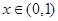
时,函数
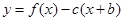
的图象上任一点P处的切线斜率为k,若
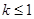
,求实数b的取值范围。
22.解:(1)

因为函数
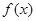
在
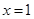
处有极值

所以

……………………3分
解得

或

………………………………4分
(i)当
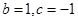
时,

所以
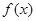
在

上单调递减,不存在极值
(ii)当

时,
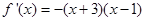

时,
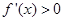
,
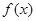
单调递增

时,

,
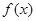
单调递减
所以
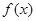
在
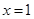
处存在极大值,符合题意
综上所述,满足条件的值为

…………7分
(2)当

时,函数
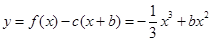
设图象上任意一点

,则
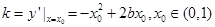
因为
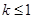
,
所以对任意

,

恒成立…………9分
所以对任意

,不等式
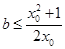
恒成立
设
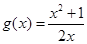
,则

当

时,

故
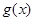
在区间

上单调递减
所以对任意

,

……………………12分

所以

……………………………

…14分
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:单选题
设
f0(
x)=
sinx,
f1(
x)=
f0′(
x),
f2(
x)=
f1′(
x),…,
fn+1(
x)=
fn′(
x),
n∈N,则
f2006(
x)=( )
| A.sinx | B.-sinx | C.cosx | D.-cosx |
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题满分13分)已知函数
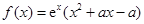
,其中
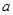
是常数.
(Ⅰ)当
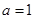
时,求
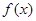
在点
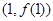
处的切线方程;
(Ⅱ)求
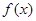
在区间
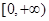
上的最小值.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
曲线
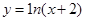
在点P(-1,0)处的切线方程是
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本题满分12分)
设函数
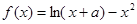
,
(1)若
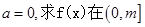
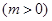
上的最大值
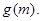
(2)若
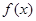
在区间[1,2]上为减函数,求a的取值范围。
(3)若直线
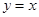
为函数
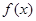
的图象的一条切线,求a的值。
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知
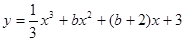
是R上的单调增函数,则
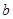
的取值范围是()
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
设
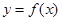
是定义在
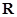
上的奇函数,
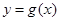
是定义在
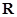
上的偶函数,且有

,(其中
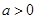
且
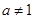
),若
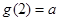
,则
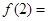
( )
查看答案和解析>>

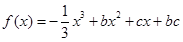 ,其导函数
,其导函数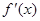 .
. 试确定b、c的值;
试确定b、c的值;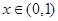 时,函数
时,函数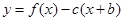 的图象上任一点P处的切线斜率为k,若
的图象上任一点P处的切线斜率为k,若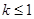 ,求实数b的取值范围。
,求实数b的取值范围。 科学实验活动册系列答案
科学实验活动册系列答案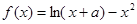 ,
,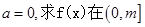
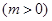 上的最大值
上的最大值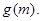
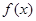 在区间[1,2]上为减函数,求a的取值范围。
在区间[1,2]上为减函数,求a的取值范围。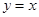 为函数
为函数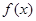 的图象的一条切线,求a的值。
的图象的一条切线,求a的值。