
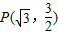 均在抛物线x2=2py上,设F为抛物线的焦点,Q为抛物线对称轴上一点,若
均在抛物线x2=2py上,设F为抛物线的焦点,Q为抛物线对称轴上一点,若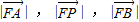 成等差数列,且
成等差数列,且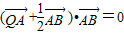 (A,B与P不重合).
(A,B与P不重合).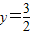 上;
上;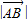 的取值范围.
的取值范围.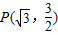 在抛物线x2=2py上,可求p,由
在抛物线x2=2py上,可求p,由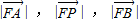 成等差数列,可得
成等差数列,可得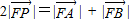 ,利用坐标表示可证
,利用坐标表示可证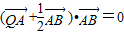 ,即
,即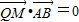 ,利用坐标表示及点A,B满足抛物线的方程联立可求
,利用坐标表示及点A,B满足抛物线的方程联立可求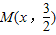 ,则可得
,则可得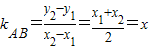 ,从而有
,从而有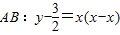 ,代入x2=2py,整理得x2-2xx+2x2-3=0,结合方程的性质及
,代入x2=2py,整理得x2-2xx+2x2-3=0,结合方程的性质及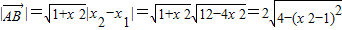 ,可求
,可求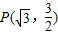 在抛物线x2=2py上,所以
在抛物线x2=2py上,所以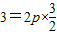 ,所以p=1.
,所以p=1.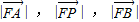 成等差数列,
成等差数列,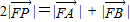 ,所以
,所以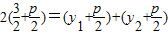 ,所以
,所以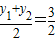 ,
,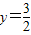 上. …(2分)
上. …(2分)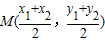 ,
,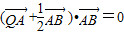 ,即
,即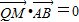 ,
,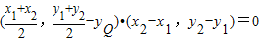 ,(x1+x2)(x2-x1)+(y1+y2-2yQ)(y2-y1)
,(x1+x2)(x2-x1)+(y1+y2-2yQ)(y2-y1)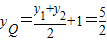 .…(6分)
.…(6分) ,
,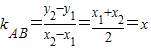 ,所以
,所以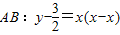 ,
,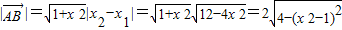 ,
,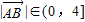 .即
.即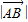 的取值范围为(0,4].…(10分)
的取值范围为(0,4].…(10分)

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
| 3 |
| 3 |
| 2 |
| FA |
| FP |
| FB |
| QA |
| 1 |
| 2 |
| AB |
| AB |
| 3 |
| 2 |
| AB |
查看答案和解析>>
科目:高中数学 来源: 题型:
已知两个动点A、B和一个定点![]() 上(A、B与M不重合).设F为抛物线的焦点,Q为对称轴上一点,若
上(A、B与M不重合).设F为抛物线的焦点,Q为对称轴上一点,若![]() ,且
,且
![]() 成等差数列.
成等差数列.
(I)求![]() 的坐标;
的坐标;
(II)若![]() ,A、B两点在抛物线
,A、B两点在抛物线![]() 准线上的射影分别为A1、B1,求四边形ABB1A1面积的取值范围.
准线上的射影分别为A1、B1,求四边形ABB1A1面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知两个动点A、B和一个定点![]() 上(A、B与M不重合).设F为抛物线的焦点,Q为对称轴上一点,若
上(A、B与M不重合).设F为抛物线的焦点,Q为对称轴上一点,若![]() ,
,
且![]() 成等差数列.
成等差数列.
(I)求![]() 的坐标;
的坐标;
(II)若![]() ,A、B两点在抛物线
,A、B两点在抛物线![]() 准线上的射影分别为A1、B1,求四边形ABB1A1面积的取值范围.
准线上的射影分别为A1、B1,求四边形ABB1A1面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年哈三中理) 已知两个动点A、B和一个定点![]() 均在抛物线
均在抛物线![]() 上(A、B与M不重合)。设F为抛物线的焦点,Q为对称轴上一点,或
上(A、B与M不重合)。设F为抛物线的焦点,Q为对称轴上一点,或![]() ,且
,且![]() 成等差数列。
成等差数列。
(1)求![]() 的坐标;
的坐标;
(2)若![]() A、B两点在抛物线
A、B两点在抛物线![]() 准线上的射影分别为
准线上的射影分别为![]() ,求四边形ABB1A1面积的取值范围。
,求四边形ABB1A1面积的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com