
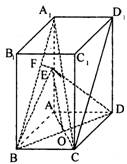
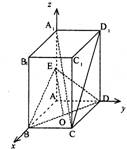
(08年三校联考)(12分) 如图,在长方体ABCD―A1B1C1D1中,棱AD=DC=3,DD1=4,E是A1A的中点.
(Ⅰ)求证:![]()
(Ⅱ)求二面角E―BD―A的大小;
(Ⅲ)求点E到平面A1BCD1的距离.

解析:解法一:
(I)连结AC交BD于点O,则O是AC的中点. 连结EO.
有A1C∥EO.
∵EO![]() 平面BED,A1C
平面BED,A1C![]() 平面BED,
平面BED,
∴A1C∥平面BED………………………………4分
(II)∵AC⊥BD于O,
又∵E是AA的中点,∴EB=ED.
∴EO⊥BD.
∴∠EOA是二面角E―BD―A的平面角.
在Rt△EAO中,EA=![]() AA1=2,AO=
AA1=2,AO=![]() AC=
AC=![]()
∴tAnEOA=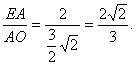
二面角E―BD―A的大小是![]() …………………………………8分
…………………………………8分
(III)过点E作EF⊥A1B于F.
∵A1D1⊥平面A1B1BA,EF![]() 平面A1B1BA,
平面A1B1BA,
∴A1D1⊥EF且A1B∩A1D1=A1.
∴EF⊥平面A1BCD1.…………………………………………………………9分
则EF的长是点E到平面A1BCD1的距离.…………………………………10分
∵![]() 且A1E=2,A1B=5,AB=3,
且A1E=2,A1B=5,AB=3,
∴EF=![]() 即点E到平面A1BCD1的距离是
即点E到平面A1BCD1的距离是![]() …………………………12分
…………………………12分
解法二:
(I)如图建立空间直角坐标系,取BD的中点O,
连结EO.
A1(0,0,4),C(3,3,0),
E(0,0,2),O(![]() …………2分
…………2分
![]() ,
,
![]() ,∴A1C∥EO.
,∴A1C∥EO.
∵EO![]() 平面BED,A1C
平面BED,A1C![]() 平面BED,
平面BED,
∴A1C∥平面BED.…………………………4分
(II)由于AE⊥平面ABCD,则![]() 就是平面ABCD的法向量.…………5分
就是平面ABCD的法向量.…………5分
B(3,0,0),D(0,3,0),![]()
设平面EBD的法向量为![]()
由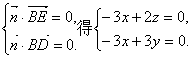
令z=3,则![]() ……………………………………………………6分
……………………………………………………6分
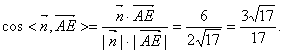
∴二面角E―BD―A的大小为arrccos ![]() .………………………………8分
.………………………………8分
(III)D1(0,3,4),则![]() ,设平面A1BCD1的法向量为
,设平面A1BCD1的法向量为![]()
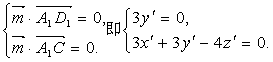
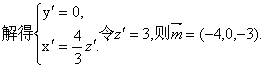
即点E到平面A1BCD1的距离是![]()
又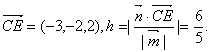 …………………………………………12分
…………………………………………12分


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:
(08年三校联考)(12分) 袋中装有黑、白球共7个,从中任取2个全是白球的概率为![]() ,现在甲、乙两人从袋中轮流摸取1个球,甲先取,乙后取,然后甲再取,
,现在甲、乙两人从袋中轮流摸取1个球,甲先取,乙后取,然后甲再取,![]() ,取后不放回,两人中有一个人取到白球时即终止.每个球在第一次被取到的机会相同.
,取后不放回,两人中有一个人取到白球时即终止.每个球在第一次被取到的机会相同.
(Ⅰ)求袋中白球的个数;
(Ⅱ)求甲取到白球的概率.
(Ⅲ)(理)用![]() 表示取球终止时的取球次数,求
表示取球终止时的取球次数,求![]() 的概率分布和期望;
的概率分布和期望;
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年三校联考理) 已知函数![]() 在
在![]() 处取得极值
处取得极值![]() ,其中a、b为常数.
,其中a、b为常数.
(Ⅰ)试确定a、b的值;
(Ⅱ)讨论函数![]() 的单调区间;
的单调区间;
(Ⅲ)若对任意![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年三校联考)(12分) 已知抛物线![]() 的焦点为F,M是抛物线上纵坐标为2的点,且
的焦点为F,M是抛物线上纵坐标为2的点,且![]()
(Ⅰ)求抛物线的方程;
(Ⅱ)若该抛物线上两点![]() 关于直线
关于直线![]() 对称,
对称,
且![]() 求m的值。
求m的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com