
����Ŀ����ͼ����Բ ![]() ����ΪF1 �� �ҽ���ΪF2 �� ��F1��ֱ�߽���Բ��A��B���㣬��ABF2���ܳ�Ϊ8���ҡ�AF1F2������ʱ����AF1F2Ϊ�������Σ�
����ΪF1 �� �ҽ���ΪF2 �� ��F1��ֱ�߽���Բ��A��B���㣬��ABF2���ܳ�Ϊ8���ҡ�AF1F2������ʱ����AF1F2Ϊ�������Σ� 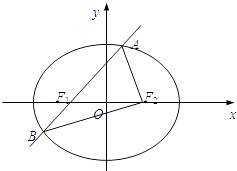
��1������ԲE�ķ��̣�
��2���趯ֱ��l��y=kx+m����ԲE����ֻ��һ��������P������ֱ��x=4�ཻ�ڵ�Q����̽��������PQΪֱ����Բ��x���λ�ù�ϵ�� ��������ƽ�����Ƿ���ڶ���M��ʹ����PQΪֱ����Բ�����M�������ڣ����M�����ꣻ�������ڣ�˵�����ɣ�
���𰸡�
��1���⣺�ߡ�ABF2���ܳ�Ϊ8����4a=8����a=2��
�ֵ���AF1F2������ʱΪ�������Σ���A��0��b����a=2c����c=1��b2=3��
����ԲE�ķ���Ϊ ![]()
��2���⣺���� 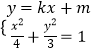 ���÷��̣�4k2+3��x2+8kmx+4m2��12=0
���÷��̣�4k2+3��x2+8kmx+4m2��12=0
��ֱ������Բ���е�m��0����=0��4k2��m2+3=0��
��� ![]() ��Q��4��4k+m����PQ�е㵽x�����
��Q��4��4k+m����PQ�е㵽x����� ![]() ��
��
����Բ��x���ཻ��
�ڼ���ƽ���ڴ��ڶ���M�����������ɶԳ���֪��M��x���ϣ����M����ΪM��x1��0���� ![]() ��
��
�� ![]() ����
���� ![]() ��
��
�� ![]() ����x1=1��
����x1=1��
���Զ���ΪM��1��0����
����������1��������Բ�Ķ��塢�ȱ������ε����ʼ��ɵó�����2�����ж�Բ�ĵ�x��ľ�����뾶�Ĵ�С��ϵ���ɵó��� �ڼ���ƽ���ڴ��ڶ���M�������������ɶԳ���֪��M��x���ϣ�������ֱ�����Ե�Բ�ܽ���ֱ�Ǽ��������
�����㾫�������ڱ��⿼�����Բ�ı����̣���Ҫ�˽���Բ�����̽�����x�![]() ��������y�
��������y�![]() ���ܵó���ȷ�𰸣�
���ܵó���ȷ�𰸣�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ABC���ڽ�A��B��C���ڽǶԱ߷ֱ�Ϊa��b��c�����㣨a+b+c����a��b+c��=ac�� ������B��
������sinAsinC= ![]() ����C��
����C��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ ![]() ����
���� ![]()
��1���� ![]() ʱ���ⲻ��ʽ
ʱ���ⲻ��ʽ ![]() ��
��
��2��![]() ��
�� ![]() ���������ʵ��
���������ʵ�� ![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������סHС������������C�Ƽ������Ӽҿ�������˾�ϰ�·����L1��L2����·�ߣ�L1·������A1��A2��A3����·�ڣ���·��������Ƶĸ��ʾ�Ϊ ![]() ��L2·������B1��B2����·�ڣ���·��������Ƶĸ�������Ϊ
��L2·������B1��B2����·�ڣ���·��������Ƶĸ�������Ϊ ![]() ��
�� ![]() ��
�� 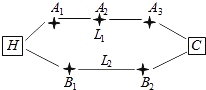
��1������L1·�ߣ����������1�κ�Ƶĸ��ʣ�
��2������L2·�ߣ���������ƴ���X����ѧ������
��3�����ա�ƽ��������ƴ������١���Ҫ�������������������������·����ѡ��һ����õ��ϰ�·�ߣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x��=|x��a|��a��R�� ����a=2ʱ���ⲻ��ʽ��f��x����6��|2x��5|��
����������x�IJ���ʽf��x����4�Ľ⼯Ϊ[��1��7]����������s��t����2s+t=a����֤�� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���A����B����C���Եı߷ֱ���a��b��c��MΪBC���е㣬BM=MC=2��AM=b��c�����ABC������ֵΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ABCD��A1B1C1D1�У�AB��BC��2��D1D��3����M��B1C1���е㣬��N��AB���е㣮������ͼ��ʾ�Ŀռ�ֱ������ϵ.
��1��д����D��N��M�����ꣻ
��2�����߶�MD��MN�ij��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ȱ�����{an}���㣬a2=3��a5=81��
��1��������{an}��ͨ�ʽ��
��2����bn=log3an �� ��{bn}��ǰn���ΪSn ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com