
【题目】通过研究学生的学习行为,心理学家发现,学生接受能力依赖于老师引入概念和描述问题所用的时间,讲座开始时,学生的兴趣激增,中间有一段不太长的时间,学生的兴趣保持理想的状态,随后学生的注意力开始分散,分析结果和实验表明,用![]() 表示学生掌握和接受概念的能力(
表示学生掌握和接受概念的能力(![]() 的值越大,表示接受能力越强),
的值越大,表示接受能力越强),![]() 表示提出和讲授概念的时间(单位:分),可以有以下公式:
表示提出和讲授概念的时间(单位:分),可以有以下公式: 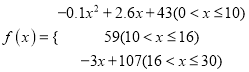 .
.
(1)开讲多少分钟后,学生的接受能力最强?能维持多少分钟?
(2)开讲5分钟与开讲20分钟比较,学生的接受能力何时强一些?
(3)一个数学难题,需要55的接受能力以及13分钟的时间,老师能否及时在学生一直达到所需接受能力的状态下讲授完这个难题?
【答案】(1)能维持6分钟时间(2)开讲5分钟时学生的接受能力比开讲20分钟时要强一些(3)来不及
【解析】试题分析:(1)当![]() 时,函数为二次函数,对称轴为
时,函数为二次函数,对称轴为![]() ,开口向下故在这个区间上单调递增,当
,开口向下故在这个区间上单调递增,当![]() 时取得最大值为
时取得最大值为![]() .当
.当![]() 时,函数为减函数,且
时,函数为减函数,且![]() ,故开讲
,故开讲![]() 分钟后达到最大值,维持
分钟后达到最大值,维持![]() 分钟.(2)通过比较
分钟.(2)通过比较![]() 的值可知开讲
的值可知开讲![]() 分钟时接受能力更强.(3)在区间
分钟时接受能力更强.(3)在区间![]() 上分别令函数值为
上分别令函数值为![]() ,求得对应的时间,作差后可知老师来不及讲授完.
,求得对应的时间,作差后可知老师来不及讲授完.
试题解析:
(1)当![]() 时,
时, ![]()
故![]() 在
在![]() 时递增,最大值为
时递增,最大值为![]()
当![]() 时,
时, ![]()
当![]() 时,
时, ![]() 为减函数,且
为减函数,且![]()
因此,开讲10分钟后,学生达到最强接受能力(为59),能维持6分钟时间.
(2)![]()
![]()
故开讲5分钟时学生的接受能力比开讲20分钟时要强一些
(3)当![]() 时,令
时,令![]() ,解得
,解得![]() 或20(舍)
或20(舍)
当![]() 时,令
时,令![]() ,解得
,解得![]()
因此学生达到(含超过)55的接受能力的时间为![]() (分)
(分)
老师来不及在学生一直达到所需接受能力的状态下讲授完这个难题.


科目:高中数学 来源: 题型:
【题目】如果y=f(x)的定义域为R,对于定义域内的任意x,存在实数a使得f(x+a)=f(﹣x)成立,则称此函数具有“P(a)性质”.给出下列命题:
①函数y=sinx具有“P(a)性质”;
②若奇函数y=f(x)具有“P(2)性质”,且f(1)=1,则f(2015)=1;
③若函数y=f(x)具有“P(4)性质”,图象关于点(1,0)成中心对称,且在(﹣1,0)上单调递减,则y=f(x)在(﹣2,﹣1)上单调递减,在(1,2)上单调递增;
④若不恒为零的函数y=f(x)同时具有“P(0)性质”和“P(3)性质”,函数y=f(x)是周期函数.
其中正确的是 (写出所有正确命题的编号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某港口![]() 要将一件重要物品用小艇送到一艘正在航行的轮船上.在小艇出发时,轮船位于港口
要将一件重要物品用小艇送到一艘正在航行的轮船上.在小艇出发时,轮船位于港口![]() 北偏西
北偏西![]() 且与该港口相距20海里的
且与该港口相距20海里的![]() 处,并以30海里/时的航行速度沿正东方向匀速行驶,假设该小船沿直线方向以
处,并以30海里/时的航行速度沿正东方向匀速行驶,假设该小船沿直线方向以![]() 海里/时的航行速度匀速行驶,经过
海里/时的航行速度匀速行驶,经过![]() 小时与轮船相遇.
小时与轮船相遇.
(1)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?
(2)假设小艇的最高航行速度只能达到30海里/时,试设计航行方案(即确定航行方向与航行速度的大小),使得小艇能以最短时间与轮船相遇,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体ABCD-A1B1C1D中,M为DD1的中点,O为AC的中点,AB=2.

(I)求证:BD1∥平面ACM;
(Ⅱ)求证:B1O⊥平面ACM;
(Ⅲ)求三棱锥O-AB1M的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在正方体ABCD-A1B1C1D中,S是B1D1的中点,E、F、G分别是BC、CD和SC的中点.求证:
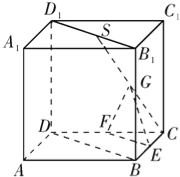
(1)直线EG∥平面BDD1B1;
(2)平面EFG∥平面BDD1B1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,公园有一块边长为2的等边三角形![]() 的地,现修成草坪,图中
的地,现修成草坪,图中![]() 把草坪分成面积相等的两部分,
把草坪分成面积相等的两部分, ![]() 在
在![]() 上,
上, ![]() 在
在![]() 上.
上.
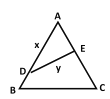
(1)设![]() ,
, ![]() ,请将
,请将![]() 表示为
表示为![]() 的函数,并求出该函数的定义域;
的函数,并求出该函数的定义域;
(2)如果![]() 是灌溉水管,为节约成本,希望它最短,
是灌溉水管,为节约成本,希望它最短, ![]() 的位置应在哪里?如果
的位置应在哪里?如果![]() 是参观线路,则希望它最长,
是参观线路,则希望它最长, ![]() 的位置又应在哪里?请予以说明.
的位置又应在哪里?请予以说明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com