
【题目】已知椭圆![]() 的左焦点在抛物线
的左焦点在抛物线![]() 的准线上,且椭圆的短轴长为2,
的准线上,且椭圆的短轴长为2,![]() 分别为椭圆的左,右焦点,
分别为椭圆的左,右焦点,![]() 分别为椭圆的左,右顶点,设点
分别为椭圆的左,右顶点,设点![]() 在第一象限,且
在第一象限,且![]() 轴,连接
轴,连接![]() 交椭圆于点
交椭圆于点![]() ,直线
,直线![]() 的斜率为
的斜率为![]() .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)若三角形![]() 的面积等于四边形
的面积等于四边形![]() 的面积,求
的面积,求![]() 的值;
的值;
(Ⅲ)设点![]() 为
为![]() 的中点,射线
的中点,射线![]() (
(![]() 为原点)与椭圆交于点
为原点)与椭圆交于点![]() ,满足
,满足![]() ,求
,求![]() 的值.
的值.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]() (Ⅲ)
(Ⅲ)![]()
【解析】
(I)根据抛物线的准线求得![]() ,根据短轴长求得
,根据短轴长求得![]() ,由此求得
,由此求得![]() ,进而求得椭圆方程.(II)设出直线
,进而求得椭圆方程.(II)设出直线![]() 的方程,联立直线
的方程,联立直线![]() 的方程和椭圆方程,求得
的方程和椭圆方程,求得![]() 点的坐标,令
点的坐标,令![]() 求得
求得![]() 点坐标.利用三角形的面积公式计算出
点坐标.利用三角形的面积公式计算出![]() 和
和![]() 的面积,根据题目已知条件,这两个三角形的面积相等,由此列方程,解方程求得
的面积,根据题目已知条件,这两个三角形的面积相等,由此列方程,解方程求得![]() 的值.(III)根据(II)求得
的值.(III)根据(II)求得![]() 点坐标,由此求得
点坐标,由此求得![]() 的斜率,设
的斜率,设![]() 所在直线方程为
所在直线方程为![]() ,代入椭圆方程,求得
,代入椭圆方程,求得![]() 点坐标,计算出
点坐标,计算出![]() 到直线
到直线![]() 的距离
的距离![]() ,
,![]() 的长度,化简
的长度,化简![]() 得到
得到![]() ,利用
,利用![]() 列方程,解方程求得
列方程,解方程求得![]() 的值.
的值.
解:(Ⅰ)由已知得,![]() ,故
,故![]() ,椭圆方程为:
,椭圆方程为:![]() ,
,
(Ⅱ)设![]() 直线方程为
直线方程为 ∴
∴![]()
∴![]() ∴
∴![]()
∴![]() ,令
,令![]() ∴
∴![]()
∴![]()
∴
∵![]() ∴
∴![]()
(Ⅲ)由(II)和中点坐标公式,得 ,设
,设![]() 所在直线方程为
所在直线方程为![]() ,则
,则
 ,∴
,∴![]() ∴
∴ ,
,
![]() 到直线
到直线![]() 的距离:
的距离: ,
,![]() ,
,
∴
即![]() ,
,
 ,化简得
,化简得![]() ,
,
∵![]() ,∴
,∴![]() .
.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:
【题目】如图①,在五边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,将
,将![]() 沿
沿![]() 折起到
折起到![]() 的位置,得到如图②所示的四棱锥
的位置,得到如图②所示的四棱锥![]() ,
,![]() 为线段
为线段![]() 的中点,且
的中点,且![]() 平面
平面![]() .
.
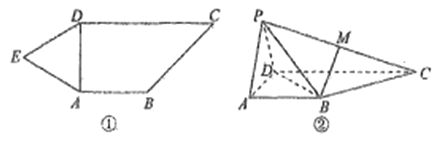
(1)求证:![]() 平面
平面![]() .
.
(2)若直线![]() 与
与![]() 所成角的正切值为
所成角的正切值为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车给市民出行带来了诸多便利,某公司购买了一批单车投放到某地给市民使用.据市场分析,每辆单车的营运累计收入![]() (单位:元)与营运天数
(单位:元)与营运天数![]() 满足
满足![]() .
.
(1)要使营运累计收入高于800元,求营运天数的取值范围;
(2)每辆单车营运多少天时,才能使每天的平均营运收入最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com