
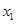 ,
,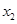 是函数
是函数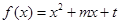 的两个零点,其中常数
的两个零点,其中常数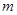 ,
,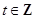 ,设
,设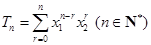 .
.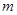 ,
,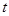 表示
表示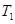 ,
,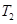 ;
;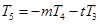 ;
;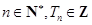 .
.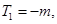
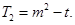 (Ⅱ)详见解析,(Ⅲ)详见解析.
(Ⅱ)详见解析,(Ⅲ)详见解析.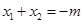 ,
,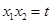 .因为
.因为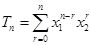 ,所以
,所以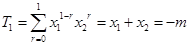 .
.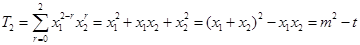 .对抽象的求和符号具体化处理,是解答本题的关键.(Ⅱ)
.对抽象的求和符号具体化处理,是解答本题的关键.(Ⅱ)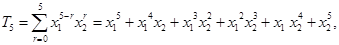 而
而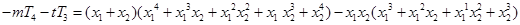
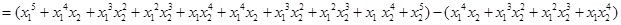
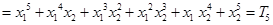 ,(Ⅲ)用数学归纳法证明有关自然数的命题. (1)当
,(Ⅲ)用数学归纳法证明有关自然数的命题. (1)当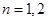 时,由(Ⅰ)问知
时,由(Ⅰ)问知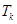 是整数,结论成立.(2)假设当
是整数,结论成立.(2)假设当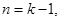
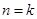 (
(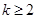 )时结论成立,即
)时结论成立,即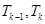 都是整数,由(Ⅱ)问知
都是整数,由(Ⅱ)问知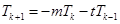 .即
.即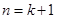 时,结论也成立.
时,结论也成立.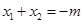 ,
,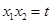 .
.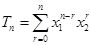 ,所以
,所以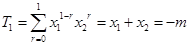 .
. 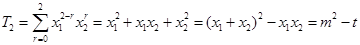 . 3分
. 3分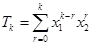 ,得
,得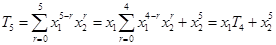 .
.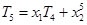 ,同理,
,同理,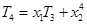 .
.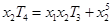 .
.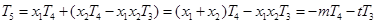 . 8分
. 8分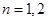 时,由(Ⅰ)问知
时,由(Ⅰ)问知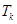 是整数,结论成立.
是整数,结论成立.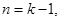
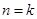 (
(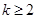 )时结论成立,即
)时结论成立,即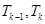 都是整数.
都是整数.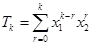 ,得
,得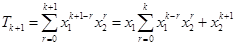 .
.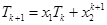 .
.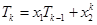 ,
,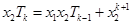 .
.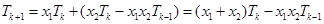 .
.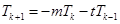 .
.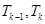 都是整数,且
都是整数,且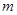 ,
,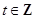 ,所以
,所以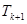 也是整数.
也是整数.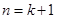 时,结论也成立.
时,结论也成立.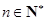 ,
,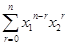 的值都是整数. 13分
的值都是整数. 13分

科目:高中数学 来源:不详 题型:解答题
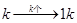 ,即当
,即当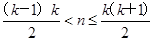 (k∈N*)时,an=(-1)k-1k,记Sn=a1+a2+…+an(n∈N*),用数学归纳法证明Si(2i+1)=-i(2i+1)(i∈N*).
(k∈N*)时,an=(-1)k-1k,记Sn=a1+a2+…+an(n∈N*),用数学归纳法证明Si(2i+1)=-i(2i+1)(i∈N*).查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.设数列﹛an﹜的前n项和为sn,由an=2n﹣1,求出s1 =12 , s2=22,s3=32,…推断sn=n2 |
B.由 cosx,满足 cosx,满足 对 对 x∈R都成立,推断 x∈R都成立,推断 为奇函数。 为奇函数。 |
C.由圆 的面积 的面积 推断:椭圆 推断:椭圆 (a>b>0)的面积s=πab (a>b>0)的面积s=πab |
| D.由(1+1)2>21,(2+1)2>22,(3+1)2 >23,…,推断对一切正整数n,(n+1)2>2n |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.2k+2 | B.2k+3 |
| C.2k+1 | D.(2k+2)+(2k+3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com